Action Value
Sources:
- Shiyu Zhao. Chapter 2: State Values and Bellman Equation. Mathematical Foundations of Reinforcement Learning.
- --> Youtube: Bellman Equation: Action Value
Action Value
From state value to action value:
- State value: the average return the agent can get starting from a state.
- Action value: the average return the agent can get starting from a state and taking an action.
Definition
Definition of action value (or action value function): \[ \begin{equation} \label{eq_def_of_action_value} q_\pi(s, a) \triangleq \mathbb{E}\left[G_t \mid S_t=s, A_t=a\right] \end{equation} \] Note:
- The \(q_\pi(s, a)\) is a function of the state-action pair \((s, a)\).
- The \(q_\pi(s, a)\) depends on \(\pi\).
Relation to the state value function
It follows from the the law of total expectation that \[ \begin{aligned} \underbrace{\mathbb{E}\left[G_t \mid S_t=s\right]}_{v_\pi(s)} = \sum_{a \in \mathcal{A}_t} \underbrace{\mathbb{E}\left[G_t \mid S_t=s, A_t=a\right]}_{q_\pi(s, a)} \pi(a \mid s) \end{aligned} \]
Hence, \[ \begin{equation} \label{eq_state_value_and_action_value} \color{orange} {v_\pi(s)=\sum_a \pi(a \mid s) q_\pi(s, a)} . \end{equation} \]
Recall the Bellman equation, the state value is given by \[ v_\pi(s)=\sum_{a \in \mathcal{A}} \pi(a \mid s)[\underbrace{\sum_r p(r \mid s, a) r+\gamma \sum_{s^{\prime}} p\left(s^{\prime} \mid s, a\right) v_\pi\left(s^{\prime}\right)}_{q_\pi(s, a)}] \]
By comparing \(\eqref{eq_state_value_and_action_value}\) and this equation, we have the action-value function as \[ \color {brown}{q_\pi(s, a)=\sum_r p(r \mid s, a) r+\gamma \sum_{s^{\prime}} p\left(s^{\prime} \mid s, a\right) v_\pi\left(s^{\prime}\right)} \] # Example
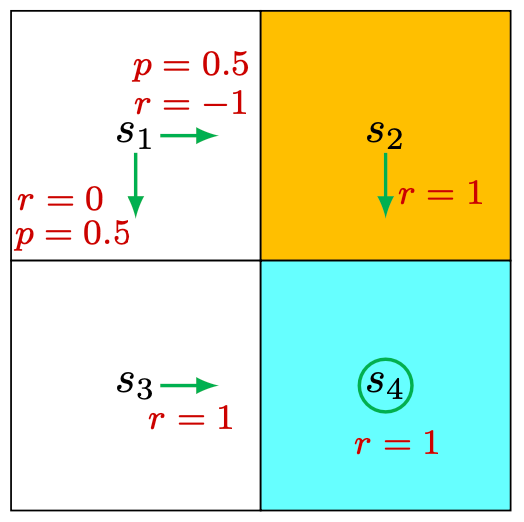
Consider the stochastic policy shown in Figure 2.8. \[ q_\pi\left(s_1, a_2\right)=-1+\gamma v_\pi\left(s_2\right) \] Note that even if an action would not be selected by a policy, it still has an action value. Therefor, for the other actions: \[ \begin{aligned} & q_\pi\left(s_1, a_1\right)=-1+\gamma v_\pi\left(s_1\right), \\ & q_\pi\left(s_1, a_3\right)=0+\gamma v_\pi\left(s_3\right), \\ & q_\pi\left(s_1, a_4\right)=-1+\gamma v_\pi\left(s_1\right), \\ & q_\pi\left(s_1, a_5\right)=0+\gamma v_\pi\left(s_1\right) . \end{aligned} \]
How to calculate action value
We can first calculate all the state values and then calculate the action values with \(\eqref{eq_verbose_def_of_action_value}\).
We can also directly calculate the action values with or without models (discussed later).