Sources:

• VICReg 2022 paper
• VC Reg, a follow-up paper of VICReg

VCReg which is quite similar to VICeg

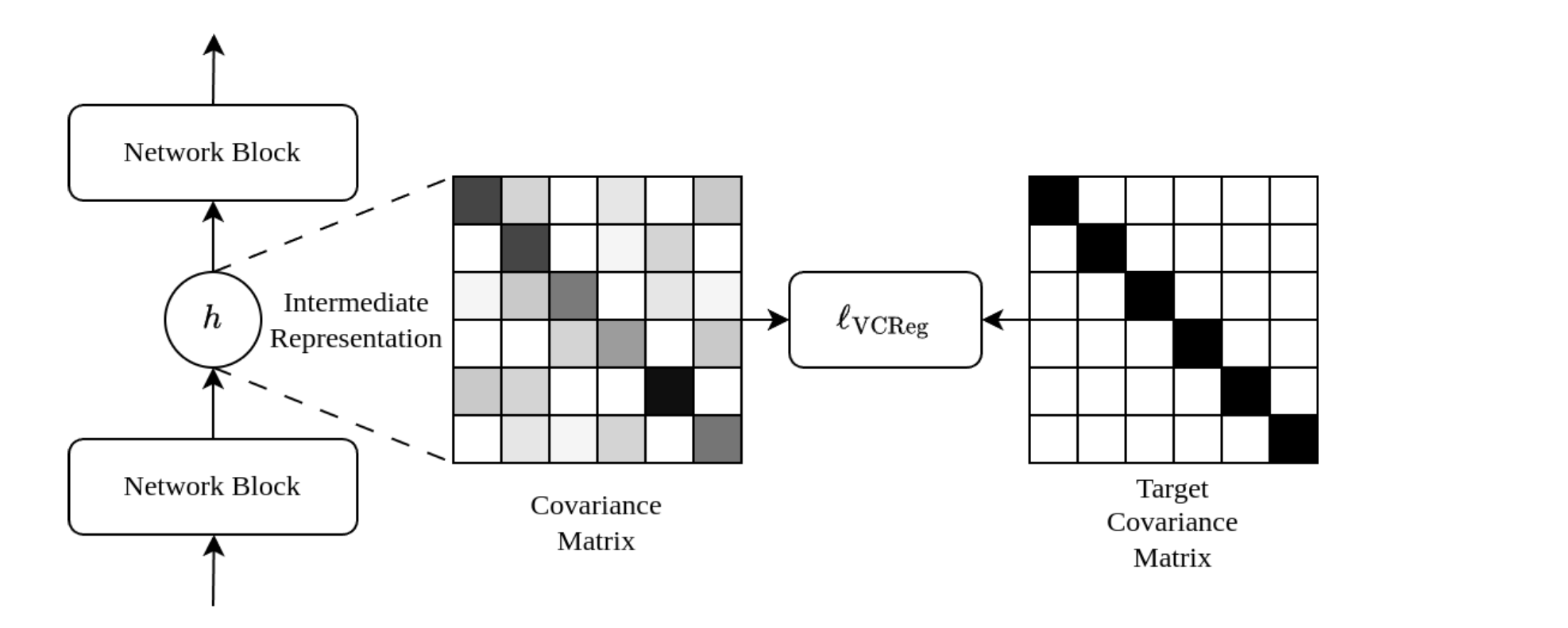
Image source: https://arxiv.org/pdf/2306.13292

Variance-Invariance-Covariance Regularization

Self-supervised learning methods aim to learn meaningful representations without relying on labels. VICReg (Variance-Invariance-Covariance Regularization) is one such method, which learns representations by optimizing three key objectives: maintaining variance, reducing covariance, and ensuring invariance between augmented views of the same input.

In this article, we focus solely on the core idea of VICReg—the design of its loss function—excluding discussions about network architectures and implementation details.

Notation

Symbol	Type	Description
$x_i$	$\mathbb{R}$	The $i$-th original input in the batch
$x_i^{\prime },x_i^{\prime \prime }$	$\mathbb{R}$	Two augmented versions of the original input $x_i$
$f_{\theta }(\cdot )$	Function	Neural network parameterized by $\theta$, used to generate embeddings
$z_i^{\prime },z_i^{\prime \prime }$	${\mathbb{R}}^d$	Representations of $x_i^{\prime }$ and $x_i^{\prime \prime }$ generated by $f_{\theta }$
$Z^{\prime },Z^{\prime \prime }$	${\mathbb{R}}^{d\times n}$	Batch embeddings for augmented inputs, where $Z^{\prime },Z^{\prime \prime }\in {\mathbb{R}}^{d\times n}$
$z^{\prime j},z^{\prime \prime j}$	${\mathbb{R}}^n$	The $j$-th row of $Z^{\prime }$ or $Z^{\prime \prime }$, representing values for the $j$-th dimension across all samples
$\mathrm{Cov}(Z^{\prime })$	${\mathbb{R}}^{d\times d}$	Variance-covariance matrix of $Z^{\prime }$
$\mathrm{Var}(z^{\prime j})$	$\mathbb{R}$	Variance of the $j$-th dimension across embeddings in $Z^{\prime }$
$\gamma$	$\mathbb{R}$	Threshold for variance regularization (e.g., $\gamma =1$)
$\ell (Z^{\prime },Z^{\prime \prime })$	$\mathbb{R}$	Overall VICReg loss function
$v(Z^{\prime }),c(Z^{\prime }),s(Z^{\prime },Z^{\prime \prime })$	$\mathbb{R}$	Variance loss, covariance loss, and invariance loss, respectively
$\mu ,\nu ,\lambda$	$\mathbb{R}$	Hyperparameters controlling the weight of variance, covariance, and invariance terms

Abbreviations

Abbreviation	Description
VICReg	Variance-Invariance-Covariance Regularization
Cov	Covariance
Var	Variance
NN	Neural network

Problem setting

We consider a batch of data $\{x_1,\dots ,x_n\}$. For each sample $x_i$, two augmented views $x_i^{\prime }$ and $x_i^{\prime \prime }$ are generated. These augmentations are passed through a neural network $f_{\theta }(\cdot )$, producing embeddings:

$$z_i^{\prime }=f_{\theta }\left(x_i^{\prime }\right)\text{ and }{z}_i^{\prime \prime }=f_{\theta }\left(x_i^{\prime \prime }\right)$$

where $z_i^{\prime },z_i^{\prime \prime }\in {\mathbb{R}}^d$. The embeddings for the entire batch are represented as two matrices:

$$Z^{\prime }=[z_1^{\prime },z_2^{\prime },\dots ,z_n^{\prime }]\text{ and }{Z}^{\prime \prime }=[z_1^{\prime \prime },z_2^{\prime \prime },\dots ,z_n^{\prime \prime }]$$

where $Z^{\prime },Z^{\prime \prime }\in {\mathbb{R}}^{d\times n}$.

The variance-covariance matrix of $Z^{\prime }$ is defined as:

$$\mathrm{Cov}\left(Z^{\prime }\right)=\mathbb{E}\left[(Z^{\prime }-\mathbb{E}\left[Z^{\prime }\right]){(Z^{\prime }-\mathbb{E}\left[Z^{\prime }\right])}^T\right]$$

Expanding this:

$$\mathrm{Cov}\left(Z^{\prime }\right)=\left[\begin{array}{ccc}\mathrm{Cov}(z_1^{\prime },z_1^{\prime })& \cdots & \mathrm{Cov}(z_1^{\prime },z_n^{\prime })\\ ⋮& \ddots & ⋮\\ \mathrm{Cov}(z_n^{\prime },z_1^{\prime })& \cdots & \mathrm{Cov}(z_n^{\prime },z_n^{\prime })\end{array}\right]$$

VICReg loss

VICReg optimizes three goals:

1. High Variance: Encourage $\mathrm{Var}\left(z^{\prime j}\right)$ to prevent collapse, where all embeddings $z_i^{\prime }$ become identical. For example, if all embeddings are mapped to the same vector $[1,2,\dots ,d]$: $$Z^{\prime }=\left[\begin{array}{cccc}1& 1& \cdots & 1\\ 2& 2& \cdots & 2\\ ⋮& ⋮& \ddots & ⋮\\ d& d& \cdots & d\end{array}\right]$$ In this case, each dimension $z^{\prime j}$ (e.g., $z^{\prime 1}=[1,1,\dots ,1]$) has no variation, resulting in: $$\mathrm{Var}\left(z^{\prime j}\right)=0\mathrm{\forall }j$$ To prevent this, VICReg introduces the variance loss¹: $$v\left(Z^{\prime }\right)=\frac{1}{d}\sum _{j=1}^{d}max(0,\gamma -\mathrm{Var}\left(z^{\prime j}\right))$$

2. Low Covariance: Minimize off-diagonal elements of $\mathrm{Cov}\left(Z^{\prime }\right)$. The covariance loss: $$c\left(Z^{\prime }\right)=\frac{1}{d}\sum _{i\ne j}{\left[\mathrm{Cov}\left(Z^{\prime }\right)\right]}_{i,j}^2$$ This reduces redundancy by minimizing overlap between dimensions.

3. Invariance: Ensure embeddings $Z^{\prime }$ and $Z^{\prime \prime }$ of the same input are similar. The invariance loss: $$s(Z^{\prime },Z^{\prime \prime })=\frac{1}{n}\sum _{i=1}^n{\Vert z_i^{\prime }-z_i^{\prime \prime }\Vert }_2^2$$ This loss term is where contrastive learning resides: pushing two positive embeddings closer.

The overall VICReg loss: $$\ell (Z^{\prime },Z^{\prime \prime })=\mu [v\left(Z^{\prime }\right)+v\left(Z^{\prime \prime }\right)]+\nu [c\left(Z^{\prime }\right)+c\left(Z^{\prime \prime }\right)]+\lambda s(Z^{\prime },Z^{\prime \prime })$$ where $\lambda ,\mu$ and $\nu$ are hyperparameters controlling the importance of each term in the loss.

My comment

Invariance term is contrastive learning. Other two terms are heuristic tricks.

---

1. In the original paper, $\mathrm{Var}\left(z^{\prime j}\right)$ is replaced by $$, where $ϵ$ is a small constant for numerical stability. This is an engineering choice and does not affect the core idea. In this article, we use the simpler version for clarity and intuitiveness.↩︎