Sparse Coding
Source:
- Yubei Chen's talk on unsupervised learning.
Most of the figures in this article are sourced from Yubei Chen's course, EEC289A, at UC Davis.
Intuition of sparse coding
Back in 1972, Horace Basil Barlow proposed the Efficient coding principle:
The sensory system is organized to achieve as complete a representation of the sensory stimulus as possible with the minimum number of active neurons.
The property of representing a sensory signal with the fewest possible neurons is known as the sparsity of neural activity.
In neuroscience, it has been observed that signals post-LGN (Lateral Geniculate Nucleus) experience a dimensional increase of hundreds or thousands of times, and their activity1 becomes sparse.
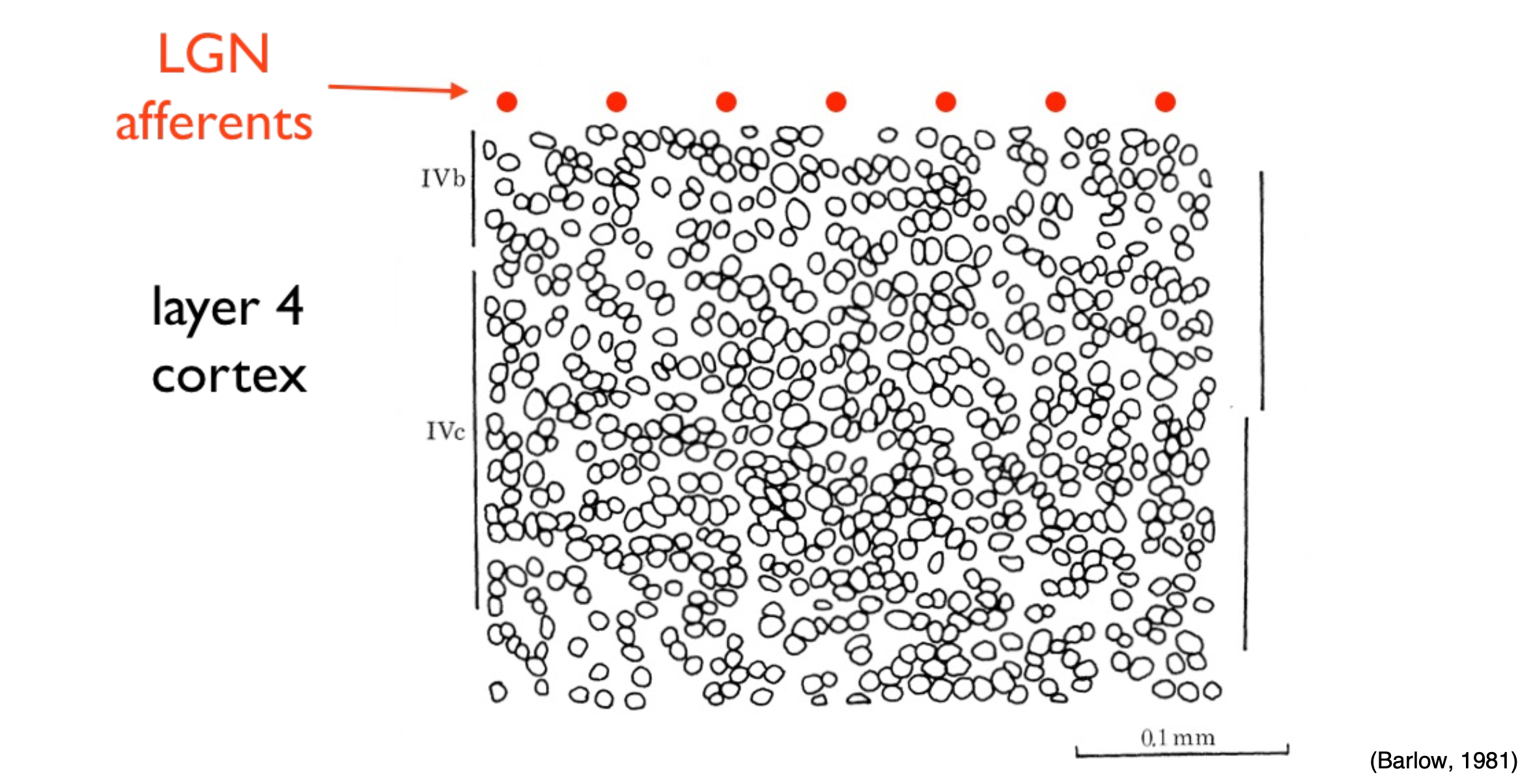
Process of sparse coding
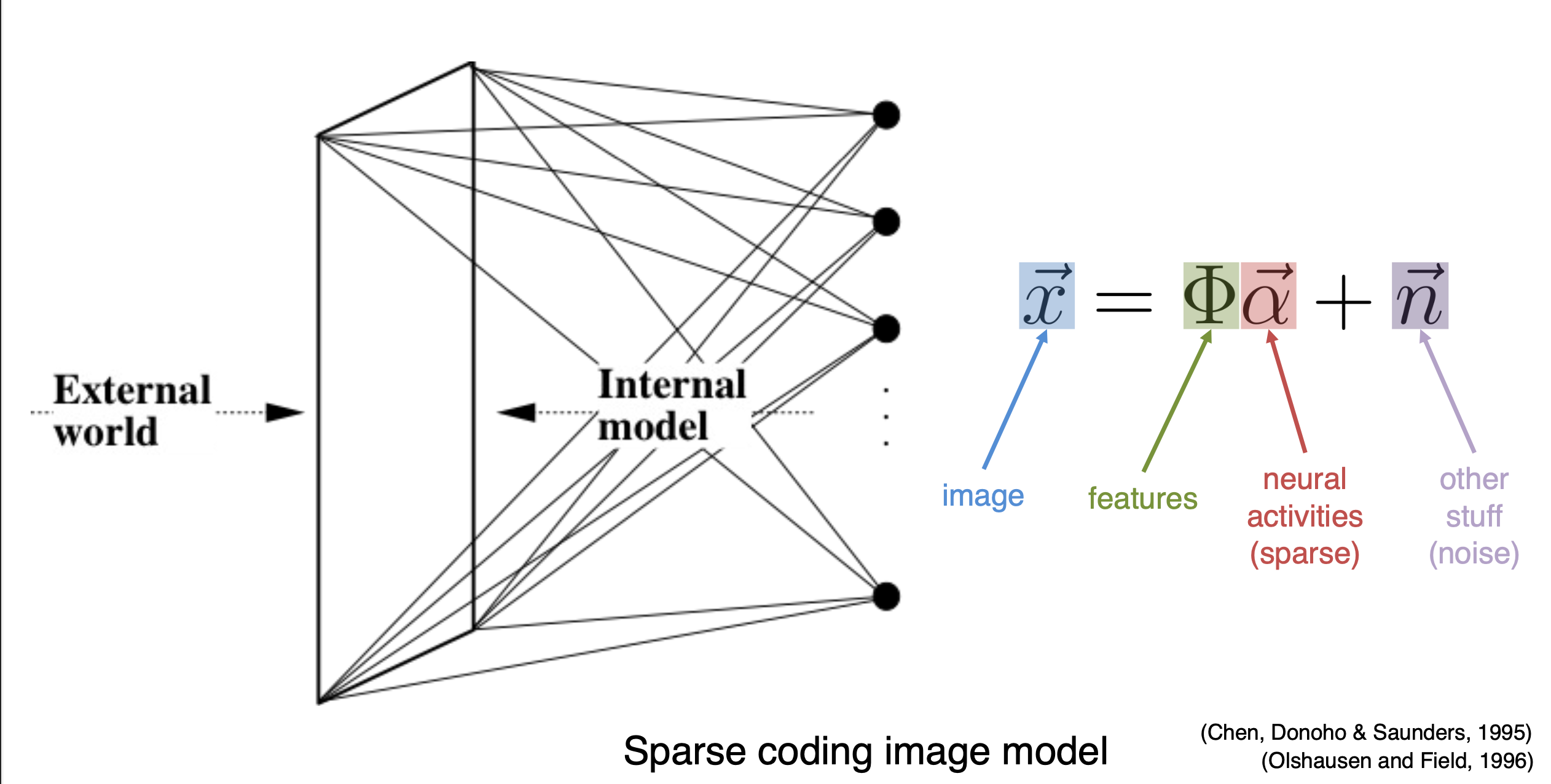
Sparse coding aims to represent each input data point, denoted as \(\vec{x}\), through a transformation involving a set of features \(\Phi\):
\[ \begin{equation} \label{eq1} \vec{x}=\Phi \vec{\alpha}+\vec{n} . \end{equation} \] In this framework, the features \(\Phi\) are common and reusable across different instances.
Meanwhile, it is essential that the composition (or activity) of \(\Phi\) MUST be sparse. This implies that \(\vec{x}\) should be constituted by the fewest number of features possible. Consequently, in \(\eqref{eq1}\), the coefficients \(\vec{\alpha}\) should have only a minimal number of non-zero entries.
Here, the activity of signals means the activity of the neurons reacting to the signals.↩︎