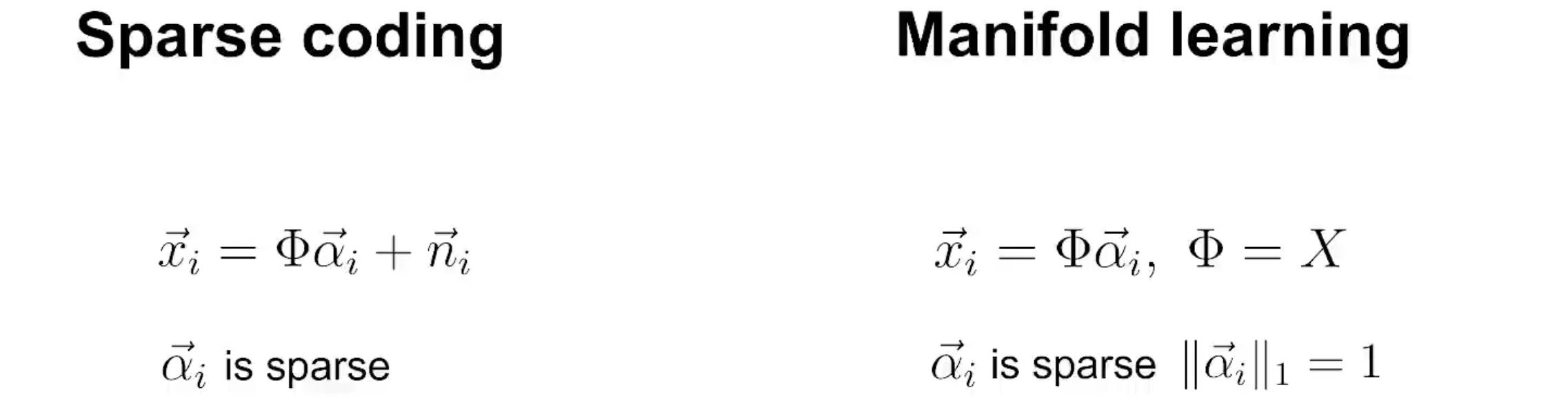Manifold Learning
Source:
- Yubei Chen's talk on unsupervised learning.
- Nonlinear Dimensionality Reduction by Locally Linear Embedding 2000 paper.
Most of the figures in this article are sourced from Yubei Chen's course, EEC289A, at UC Davis.
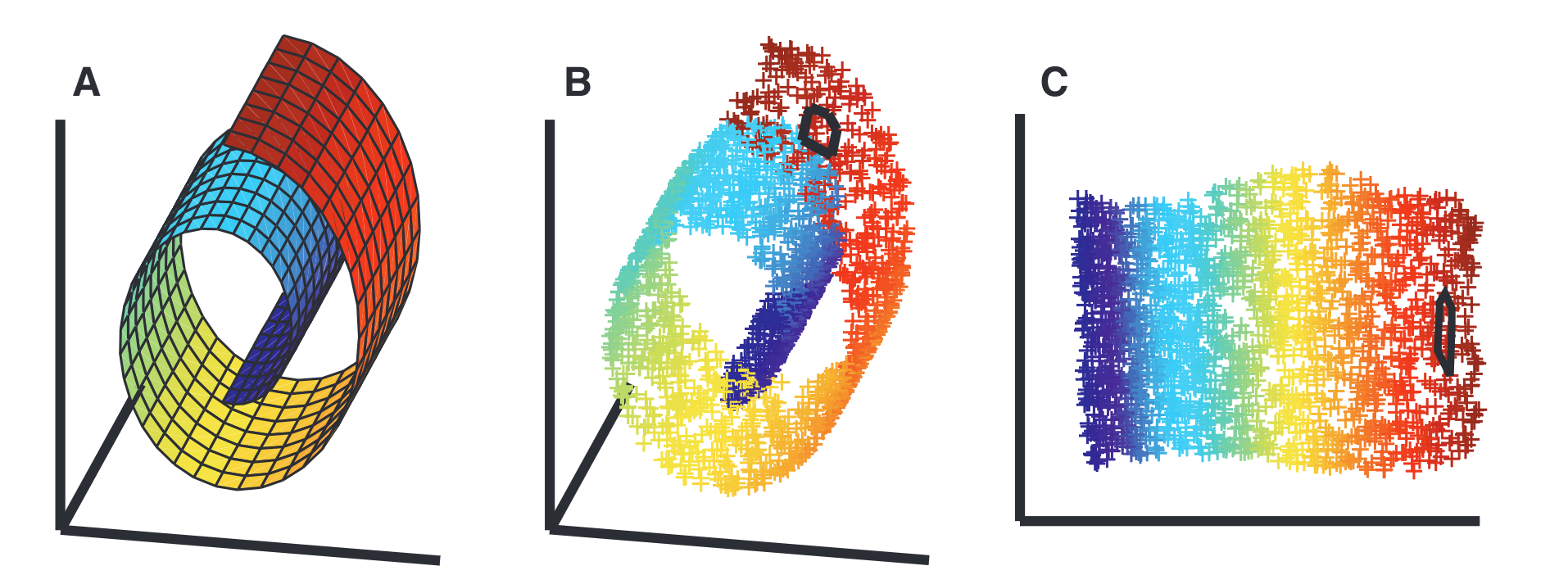
Intuition of manifold learning
I'll leave this part out since manifold learning is very common.
An explanation of manifold learning
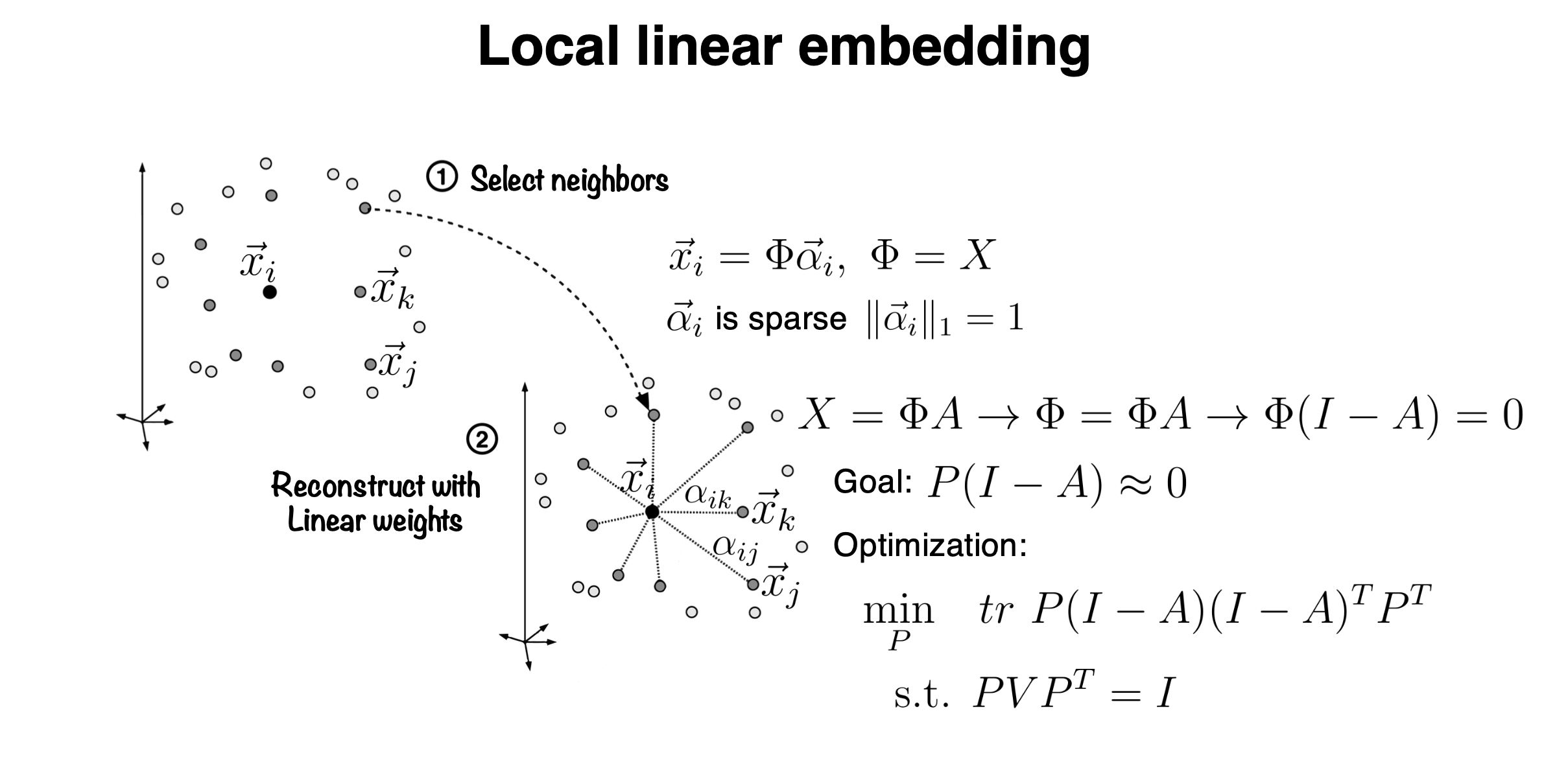
Manifold learning consists of two steps:
For every input data point \(\vec{x_i}\), identify its neighbors in the original dataset such that \(\vec{x_i}\) can be linearly represented by these neighbors (or through local linear interpolation). This corresponds to learning an optimal \(\vec{\alpha_i}\) such that \[ \begin{equation} \label{eq1} \vec{x}_i=\Phi \vec{\alpha_i}, \Phi=X . \end{equation} \] Note that we also impose a sparsity condition on \(\vec{\alpha_i}\), as we are specifically looking for neighbors. Thus, the neighbors of \(\vec{x_i}\) in the original dataset should only be a few.
The next step involves dimensionality reduction of the data space, aiming to preserve the local linearity identified in the first step within the reduced-dimensional space."
Manifold learning and sparse coding
As can be seen, the first step of manifold learning can be considered as sparse coding if we treat neighbours as features, except that it also includes a dimensionality reduction in the second step. This is also the inspiration for Yubei Chen's The Sparse Manifold Transform.