Analysis of Feedback Systems
Sources:
- B. P. Lathi & Roger Green. (2018). Chapter 4: The Laplace Transform. Signal Processing and Linear Systems (3rd ed., pp. 404-412). Oxford University Press.
Analysis of a Second-Order System
Transient response depends upon the location of poles and zeros of the transfer function \(T(s)\). In the general case, however, there is no quick way of predicting transient response parameters (PO, \(t_r, t_s\) ) from the poles and zeros of \(T(s)\). However, for a second-order system with no zeros, there is a direct relationship between the pole locations and the transient response. In such a case, the pole locations can be immediately determined from the knowledge of the transient parameter specifications. As we shall see, the study of the second-order system can be used to study many higher-order systems. For this reason, we shall now study the behavior of a second-order system in detail.
Let us consider a second-order transfer function \(T(s)\), given by \[ T(s)=\frac{\omega_n^2}{s^2+2 \zeta \omega_n s+\omega_n^2} \]
Thee settling time \(t_s\) is given by \[ t_s=\frac{4}{\zeta \omega_n} \]
To determine the PO (percent overshoot), we find \(t_p\), the peak time where the peak overshoot occurs. At \(t=t_p, d y / d t=0\). The straightforward solution of this equation yields \[ t_p=\frac{\pi}{\omega_n \sqrt{1-\zeta^2}} \] Moreover, \(\mathrm{PO}\) is given by \[ \mathrm{PO}=\frac{y\left(t_p\right)-1}{1} \times 100 \%=100 e^{-\zeta \pi / \sqrt{1-\zeta^2}} \]
Root locus
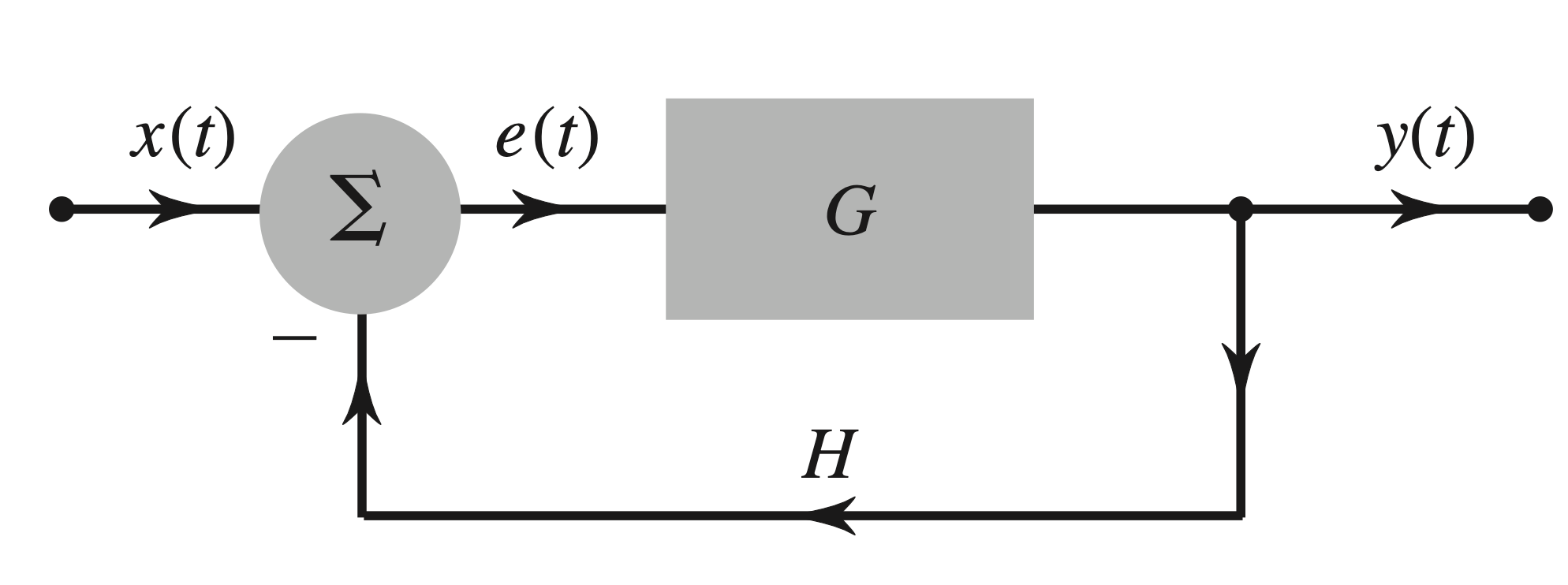
Consider the feedback amplifier in Fig. 4.34. Let the forward amplifier gain \(G=10,000\). One-hundredth of the output is fed back to the input \((H=0.01)\). The gain \(T\) of the feedback amplifier is obtained by [see Eq. (4.35)] \[ T=\frac{G}{1+G H}=\frac{10,000}{1+100}=99.01 \]
Suppose that because of aging or replacement of some transistors, the gain \(G\) of the forward amplifier changes from 10,000 to 20,000 . The new gain of the feedback amplifier is given by \[ T=\frac{G}{1+G H}=\frac{20,000}{1+200}=99.5 \]
Surprisingly, \(100 \%\) variation in the forward gain \(G\) causes only \(0.5 \%\) variation in the feedback amplifier gain \(T\). Such reduced sensitivity to parameter variations is a must in precision amplifiers.