The Sampling Theorem
Sources:
- B. P. Lathi & Roger Green. (2018). Chapter 8: Sampling: The Bridge From Continuous To Discrete. Signal Processing and Linear Systems (3rd ed., pp. 775-784). Oxford University Press.
In this article, we show that a real signal \(x(t)\) whose spectrum is bandlimited to \(B\) Hz, i.e., \(X(\omega)=0\) for \(|\omega|>2 \pi B)\), can be reconstructed exactly (without any error) from its samples taken uniformly at a rate \(f_s>2 B\) samples per second. In other words, the minimum sampling frequency is \[ f_s>2 B \] Hz.
NOTE: In some literature, \(f_s=2 B\) is be used, which is not correct.
Notation
| Symbol | Meaning |
|---|---|
| \(f_s\) | The sampling frequency in Hz. |
| \(\bar x(t)\) | The sampled signal \(\bar{x}(t)\) whereas the original signal is \(x(t)\). |
| \(\delta_T(t)\) | The impulse train signal, consisting of unit impulses repeating periodically every \(T\) seconds, |
The sampling theorem
To prove the sampling theorem, consider a signal \(x(t)\) (Fig. 8.1a) whose spectrum (Fig. 8.1b) is bandlimited to \(B\) Hz.
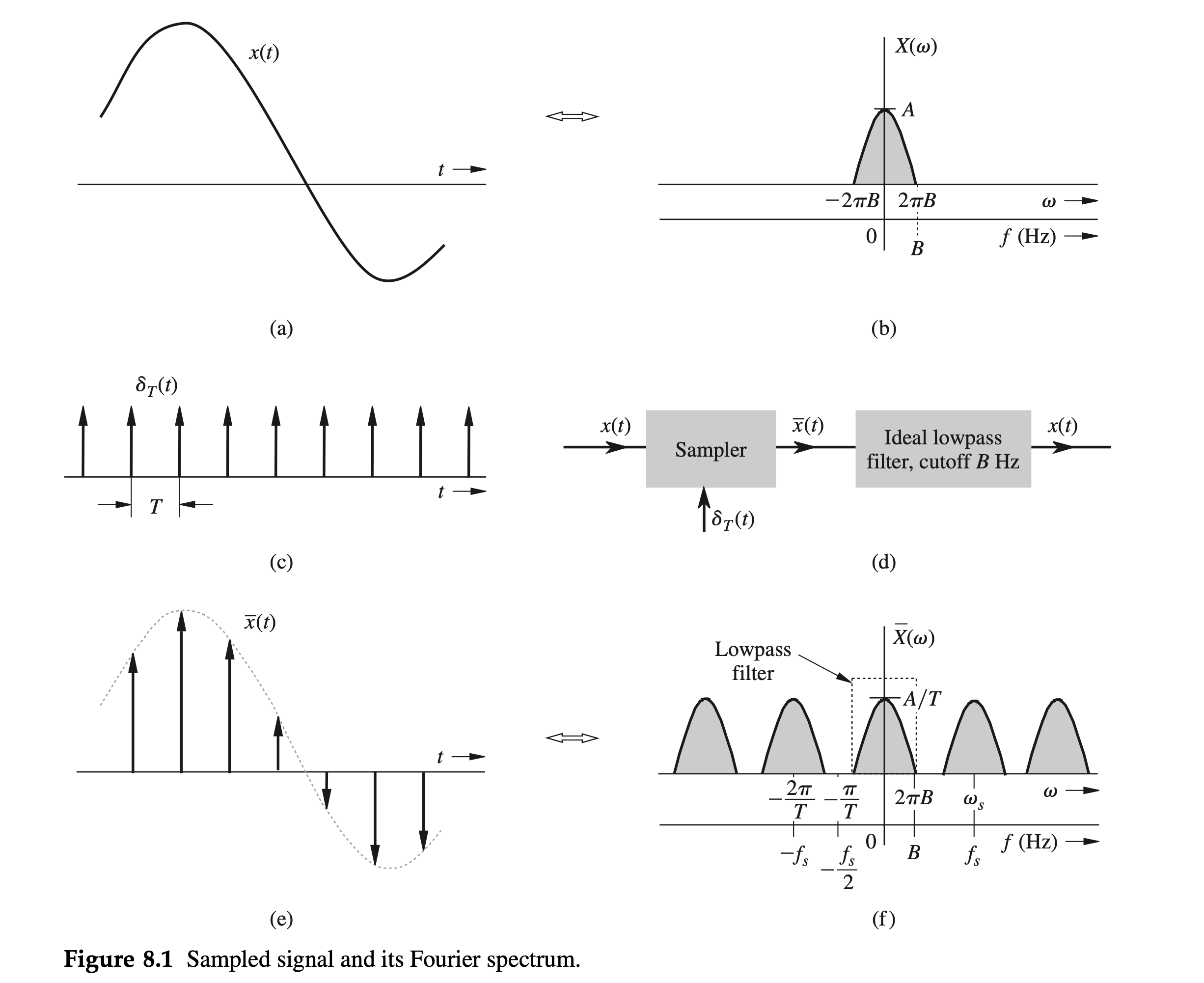
For convenience, spectra are shown as functions of \(\omega\) as well as of \(f\) (hertz).
Sampling \(x(t)\) at a rate of \(f_s\) Hz can be accomplished by multiplying \(x(t)\) by an impulse train \(\delta_T(t)\) (Fig. 8.1c), consisting of unit impulses repeating periodically every \(T\) seconds, where \(T=1 / f_s\). The schematic of a sampler is shown in Fig. 8.1d. The resulting sampled signal \(\bar{x}(t)\) is shown in Fig. 8.1e.
The sampled signal consists of impulses spaced every \(T\) seconds (the sampling interval). The \(n\)th impulse, located at \(t=n T\), has a strength \(x(n T)\), the value of \(x(t)\) at \(t=n T\). \[ \color{green} {\bar{x}(t)=x(t) \delta_T(t)=\sum_n x(n T) \delta(t-n T)} \]
Because the impulse train \(\delta_T(t)\) is a periodic signal of period \(T\), it can be expressed as a trigonometric Fourier series: \[ \delta_T(t)=\frac{1}{T}\left[1+2 \cos \omega_s t+2 \cos 2 \omega_s t+2 \cos 3 \omega_s t+\cdots\right] \quad \omega_s=\frac{2 \pi}{T}=2 \pi f_s \]
Therefore, \[ \color{green} {\bar{x}(t)=x(t) \delta_T(t)=\frac{1}{T}\left[x(t)+2 x(t) \cos \omega_s t+2 x(t) \cos 2 \omega_s t+2 x(t) \cos 3 \omega_s t+\cdots\right]} \]
To find \(\bar{X}(\omega)\), the Fourier transform of \(\bar{x}(t)\), we take the Fourier transform of the right-hand side of this equation, term by term.
The transform of the first term in the brackets is \(X(\omega)\).
The transform of the second term \(2 x(t) \cos \omega_s t\) is \(X\left(\omega-\omega_s\right)+X\left(\omega+\omega_s\right)\). This represents spectrum \(X(\omega)\) shifted to \(\omega_s\) and \(-\omega_s\).
Similarly, the transform of the third term \(2 x(t) \cos 2 \omega_s t\) is \(X\left(\omega-2 \omega_s\right)+X\left(\omega+2 \omega_s\right)\), which represents the spectrum \(X(\omega)\) shifted to \(2 \omega_s\) and \(-2 \omega_s\), and so on to infinity.
This result means that the spectrum \(\bar{X}(\omega)\) consists of \(X(\omega)\) repeating periodically with period \(\omega_s=2 \pi / T \mathrm{rad} / \mathrm{s}\), or \(f_s=1 / T \mathrm{~Hz}\), as depicted in Fig. 8.1f. Therefore,
\[ \color{teal} {\bar{X}(\omega)=\frac{1}{T} \sum_{n=-\infty}^{\infty} X\left(\omega-n \omega_s\right)} \]
If we are to reconstruct \(x(t)\) from \(\bar{x}(t)\), we should be able to recover \(X(\omega)\) from \(\bar{X}(\omega)\). This recovery is possible if there is no overlap between successive cycles of \(\bar{X}(\omega)\). Figure 8.1f indicates that this requires \[ \begin{equation} \label{eq8_3} \color{salmon} {f_s>2 B} \end{equation} \]
Also, the sampling interval \(T=1 / f_s\). Therefore, \[ T<\frac{1}{2 B} \]
The corresponding sampling interval \(T=1 / 2 B\) is called the Nyquist interval for \(x(t)\).
Thus, as long as the sampling frequency \(f_s > 2B\) (in hertz), \(\bar{X}(\omega)\) consists of nonoverlapping repetitions of \(X(\omega)\), and \(x(t)\) can be recovered from its samples \(\bar{x}(t)\) by passing the sampled signal \(\bar{x}(t)\) through an ideal lowpass filter having a bandwidth of any value between \(B\) and \(f_s-B\) Hz.
Practical sampling
In proving the sampling theorem, we assumed ideal samples obtained by multiplying a signal \(x(t)\) by an impulse train that is physically unrealizable. In practice, we multiply a signal \(x(t)\) by a train of pulses of finite width, depicted in Fig. 8.3c. The sampler is shown in Fig. 8.3d. The sampled signal \(\bar{x}(t)\) is illustrated in Fig. 8.3e.
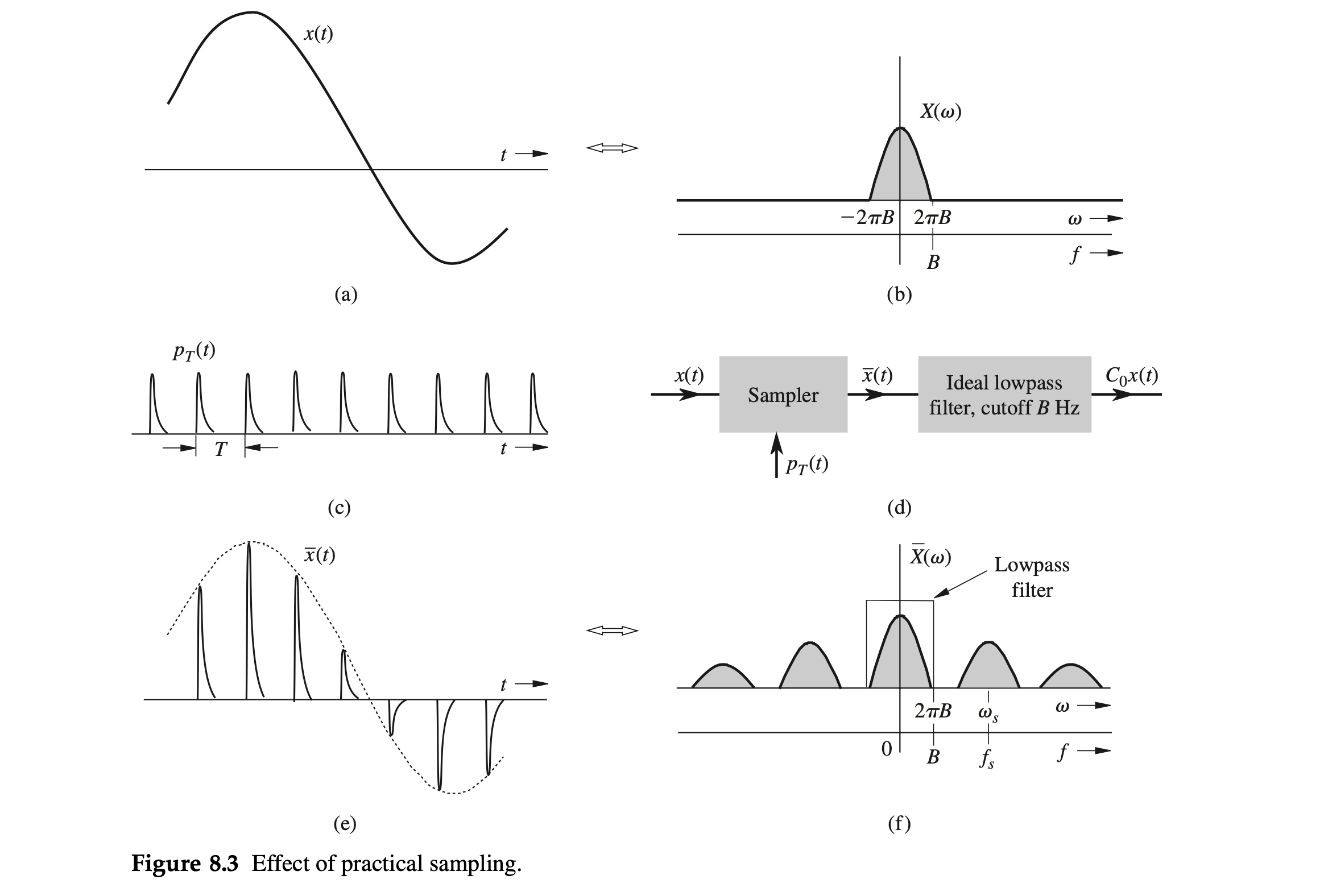
We wonder whether it is possible to recover or reconstruct \(x(t)\) from this \(\bar{x}(t)\). Surprisingly, the answer is affirmative, provided the sampling rate is not below the Nyquist rate. The signal \(x(t)\) can be recovered by lowpass filtering \(\bar{x}(t)\) as if it were sampled by impulse train.
The plausibility of this result becomes apparent when we consider the fact that reconstruction of \(x(t)\) requires the knowledge of the Nyquist sample values. This information is available or built into the sampled signal \(\bar{x}(t)\) in Fig. 8.3e because the \(n\)th sampled pulse strength is \(x(n T)\). To prove the result analytically, we observe that the sampling pulse train \(p_T(t)\) depicted in Fig. 8.3c, being a periodic signal, can be expressed as a trigonometric Fourier series \[ p_T(t)=C_0+\sum_{n=1}^{\infty} C_n \cos \left(n \omega_s t+\theta_n\right) \quad \omega_s=\frac{2 \pi}{T} \]
Thus, \[ \begin{aligned} \bar{x}(t) & =x(t) p_T(t)=x(t)\left[C_0+\sum_{n=1}^{\infty} C_n \cos \left(n \omega_s t+\theta_n\right)\right] \\ & =C_0 x(t)+\sum_{n=1}^{\infty} C_n x(t) \cos \left(n \omega_s t+\theta_n\right) \end{aligned} \]
The sampled signal \(\bar{x}(t)\) consists of \[ C_0 x(t), C_1 x(t) \cos \left(\omega_s t+\theta_1\right), C_2 x(t) \cos \left(2 \omega_s t+\theta_2\right), \ldots \] Note that the first term \(C_0 x(t)\) is the desired signal and all the other terms are modulated signals with spectra centered at \(\pm \omega_s, \pm 2 \omega_s, \pm 3 \omega_s, \ldots\), as illustrated in Fig. 8.3f.
Clearly the signal \(x(t)\) can be recovered by lowpass filtering of \(\bar{x}(t)\), as shown in Fig. 8.3d. As before, it is necessary that \(\omega_s>4 \pi B\left(\right.\) or \(\left.f_s>2 B\right)\).