The Zero-State Response
Sources:
- B. P. Lathi & Roger Green. (2021). Chapter 2: Time-Domain Analysis of Continuous-Time Systems. Signal Processing and Linear Systems (2nd ed., pp. 168-195). Oxford University Press.
This section is devoted to the determination of the zero-state response(see past post) of an LTIC system. We shall assume that the systems discussed in this section are in the zero state unless mentioned otherwise.
The zero-state response
We shall use the superposition property for finding the system response to an arbitrary input \(x(t)\).
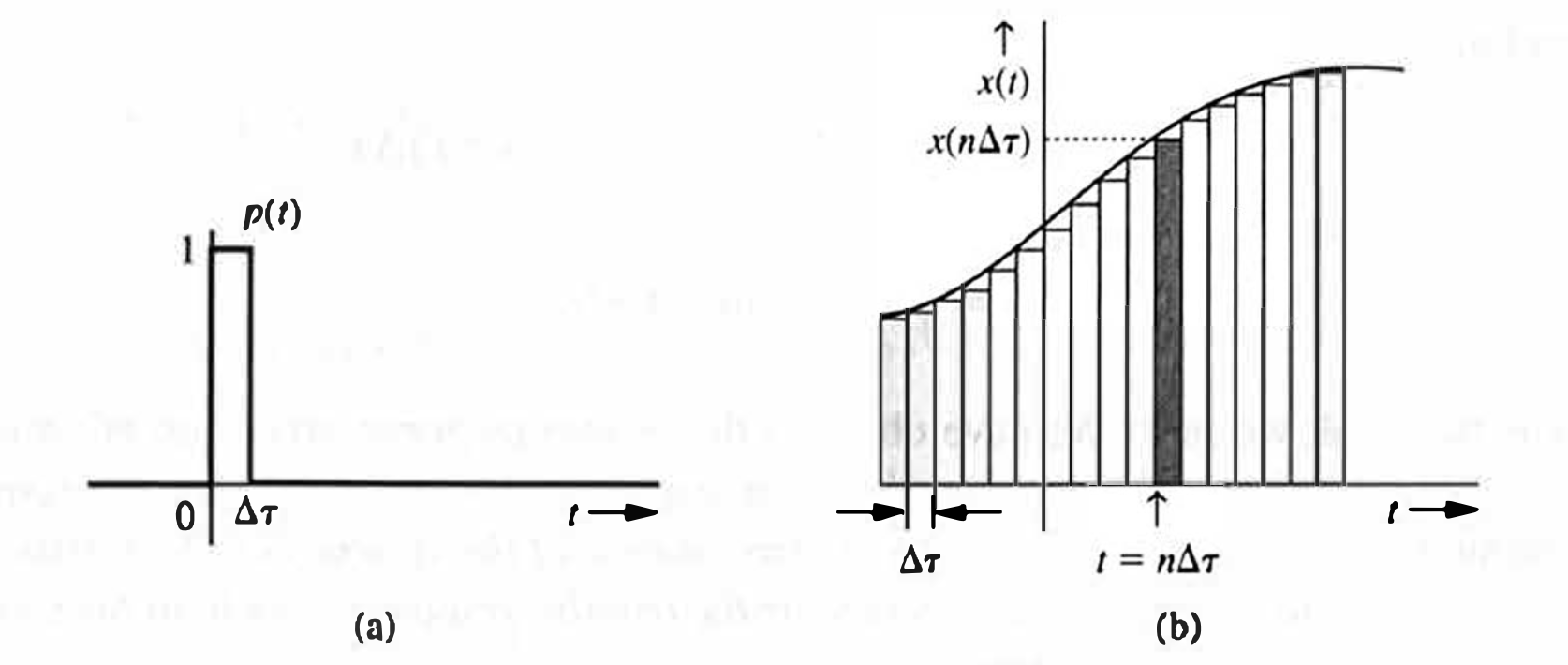
Let us define a basic pulse \(p(t)\) of unit height and width \(\Delta \tau\), starting at \(t=0\) as illustrated in Fig. 2.3a. Figure 2.3b shows an input \(x(t)\) as a sum of narrow rectangular pulses. The pulse starting at \(t=n \Delta \tau\) in Fig. 2.3b has a height \(x(n \Delta \tau)\) and can be expressed as \(\textcolor{blue} {x(n \Delta \tau) p(t-n \Delta \tau)}\). Now, \(x(t)\) is the sum of all such pulses. Hence, \[ x(t)=\lim _{\Delta \tau \rightarrow 0} \sum_\tau \textcolor{blue} {x(n \Delta \tau) p(t-n \Delta \tau)}=\lim _{\Delta \tau \rightarrow 0} \sum_\tau\left[\frac{ \textcolor{blue} {x(n \Delta \tau)}} {\Delta \tau}\right] \textcolor{blue}{ p(t-n \Delta \tau)}\Delta \tau . \]
The term \([ \frac { \textcolor{blue} { x(n \Delta \tau)} } { \Delta \tau}] \textcolor{blue} {p(t-n \Delta \tau)}\) represents a pulse \(p(t-n \Delta \tau)\) with height \([x(n \Delta \tau) / \Delta \tau]\). As \(\Delta \tau \rightarrow 0\), the height of this strip \(\rightarrow \infty\), but its area remains \(x(n \Delta \tau)\). Hence, this strip approaches an impulse \(x(n \Delta \tau) \delta(t-n \Delta \tau)\) as \(\Delta \tau \rightarrow 0\) (Fig. 2.3e)1.
Therefore, \[ \textcolor{purple} {x(t)=\lim _{\Delta \tau \rightarrow 0} \sum_\tau x(n \Delta \tau) \delta(t-n \Delta \tau) \Delta \tau }. \]
To find the response for this input \(x(t)\), we consider the input and the corresponding output pairs, as shown in Figs. 2.3c-2.3e
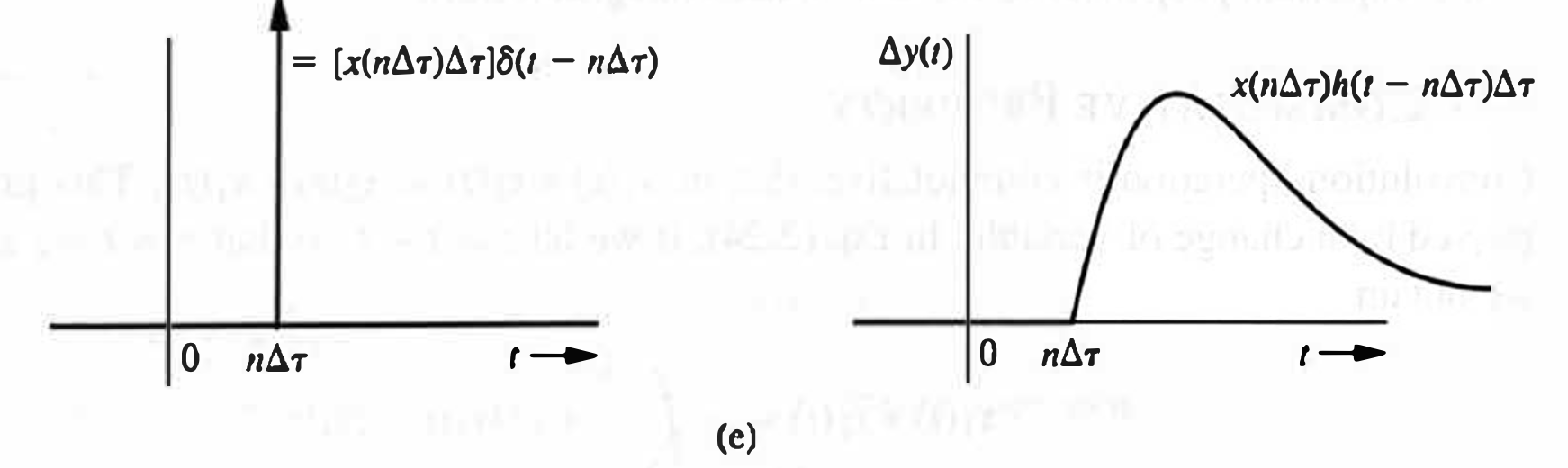
and also shown by directed arrow notation as follows: \[ \begin{aligned} \text { input } & \Longrightarrow \text { output } \\ \delta(t) & \Longrightarrow h(t) \\ \delta(t-n \Delta \tau) & \Longrightarrow h(t-n \Delta \tau) \\ {[x(n \Delta \tau) \Delta \tau] \delta(t-n \Delta \tau) } & \Longrightarrow[x(n \Delta \tau) \Delta \tau] h(t-n \Delta \tau) \\ \underbrace{\lim _{\Delta \tau \rightarrow 0} \sum_\tau x(n \Delta \tau) \delta(t-n \Delta \tau) \Delta \tau}_{x(t) \quad \text { [see Eq. (2.22)] }} & \Longrightarrow \underbrace{\lim _{\Delta \tau 0} \sum_\tau x(n \Delta \tau) h(t-n \Delta \tau) \Delta \tau}_{y(t)} \end{aligned} \]
Therefore, in a linear time-invariant (LTI) system, \[ \begin{align} & y(t) \nonumber \\ & = \textcolor{purple} {\lim _{\Delta \tau \rightarrow 0} \sum_\tau x(n \Delta \tau) h(t-n \Delta \tau) \Delta \tau} \nonumber \\ & =\textcolor{red} {\int_{-\infty}^{\infty} x(\tau) h(t-\tau) d \tau} \label{eq_2_23} \end{align} \]
Thus, we have obtained that, in a LTI system (also, recall that we have a zero-state assumption), knowing the unit impulse response \(h(t)\), we can determine the response \(y(t)\) to an arbitrary input \(x(t)\).
The LTI system assumtption is important. Linearity allowed us to use the principle of superposition, and time invariance made it possible to express the system's response to \(\delta(t-n \Delta \tau)\) as \(h(t-n \Delta \tau)\).
If the system is time-varying, then the system response to the input \(\delta(t-n \Delta \tau)\) cannot be expressed as \(h(t-n \Delta \tau)\) but instead has the form \(h(t, n \Delta \tau)\). Use of this form modifies \(\eqref{eq_2_23}\) to \[ y(t)=\int_{-\infty}^{\infty} x(\tau) h(t, \tau) d \tau \]
where \(h(t, \tau)\) is the system response at instant \(t\) to a unit impulse input located at \(\tau\).
The Convolution Integral
The zero-state response \(y(t)\) obtained in \(\eqref{eq_2_23}\) is given by an integral which is given a special name: the convolution integral.
The convolution integral of two functions \(x_1(t)\) and \(x_2(t)\) is denoted symbolically by \(\textcolor{green} {x_1(t) * x_2(t)}\) and is defined as \[ \begin{align} & x_1(t) * x_2(t) \\ & \triangleq \textcolor{green} {\int_{-\infty}^{+\infty} x_1(\tau) x_2(t-\tau) d \tau } \label{eq_2_24} . \end{align} \]
It can be proved easily that convolution is a linear operation.
Properties of the convolution integral
Some important properties of the convolution integral follow.
The Commutative Property
Convolution operation is commutative; that is, \(x_1(t) * x_2(t)=x_2(t) * x_1(t)\). This property can be proved by a change of variable. In \(\eqref{eq_2_24}\), if we let \(z=t-\tau\) so that \(\tau=t-z\) and \(d \tau=-d z\), we obtain \[ \begin{aligned} x_1(t) * x_2(t) & =-\int_{\infty}^{-\infty} x_2(z) x_1(t-z) d z \\ & =\int_{-\infty}^{\infty} x_2(z) x_1(t-z) d z \\ & =x_2(t) * x_1(t) \end{aligned} \]
The Distributive Property
According to the distributive property, \[ x_1(t) *\left[x_2(t)+x_3(t)\right]=x_1(t) * x_2(t)+x_1(t) * x_3(t) \]
The Associative Property
According to the associative property, \[ x_1(t) *\left[x_2(t) * x_3(t)\right]=\left[x_1(t) * x_2(t)\right] * x_3(t) \]
The proofs of the distributive property and the Associative Property follow directly from the definition of the convolution integral.
The Shift Property
If \[ x_1(t) * x_2(t)=c(t) \] then \[ x_1(t) * x_2(t-T)=x_1(t-T) * x_2(t)=c(t-T) \]
More generally, we see that \[ \color{brown} {x_1\left(t-T_1\right) * x_2\left(t-T_2\right)=c\left(t-T_1-T_2\right)} . \]
Proof: We are given \[ x_1(t) * x_2(t)=\int_{-\infty}^{\infty} x_1(\tau) x_2(t-\tau) d \tau=c(t) \]
Therefore, \[ \begin{aligned} x_1(t) * x_2( \textcolor{blue}{t-T}) & =\int_{-\infty}^{\infty} x_1(\tau) x_2(\textcolor{blue} {t-T}-\tau) d \tau \\ & = \textcolor{blue} {c(t-T)} . \end{aligned} \]
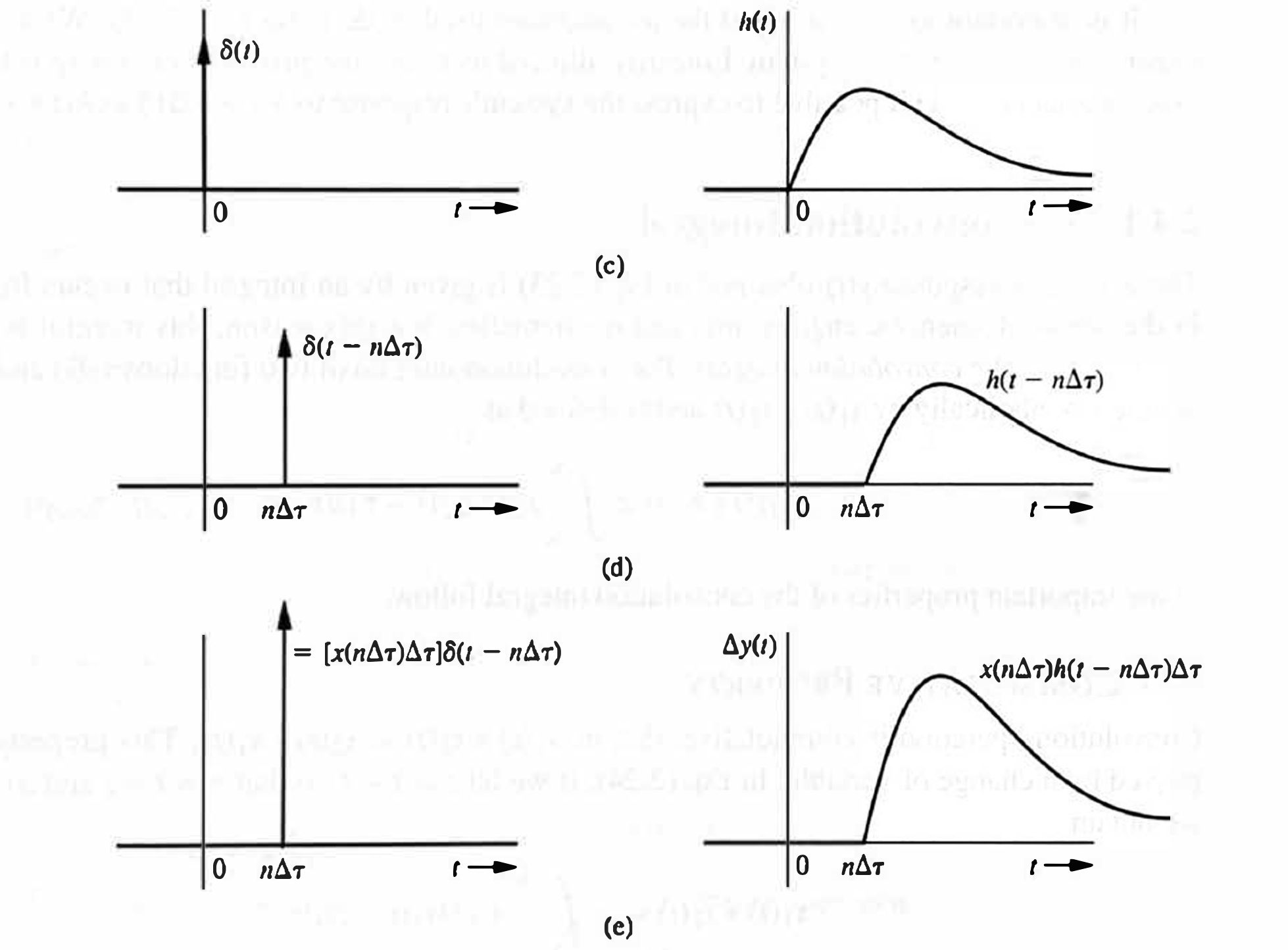
Convolution with a Unit Impulse
Convolution of a function \(x(t)\) with a unit impulse \(\delta(t)\) results in the function \(x(t)\) itself. By definition of convolution, \[ x(t) * \delta(t)=\int_{-\infty}^{+\infty} x(\tau) \delta(t-\tau) d \tau \]
Because \(\delta(t-\tau)\) is an impulse located at \(\tau=t\), according to the sampling property of the impulse (see before post, the integral here is just the value of \(x(\tau)\) at \(\tau=t\), that is, \(x(t)\). Therefore, \[ \color{orange} {x(t) * \delta(t)=x(t)} . \]
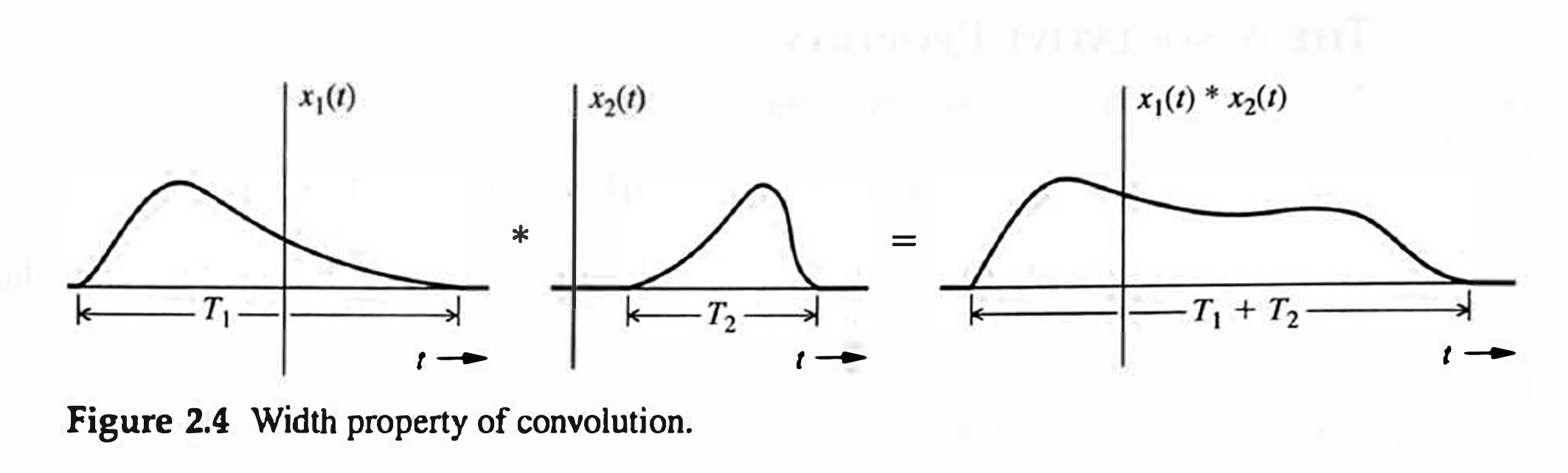
The Width Property
If the durations (widths) of \(x_1(t)\) and \(x_2(t)\) are finite, given by \(T_1\) and \(T_2\), respectively, then the duration (width) of \(x_1(t) * x_2(t)\) is \(T_1+T_2\) (Fig. 2.4). The proof of this property follows readily from the graphical considerations discussed later.
The (zero-state) response and causility
For a LTIC system, since it has already been a LTI system, its (zero-state) response \(y(t)\) is also \[ \begin{align} & y(t) \nonumber \\ & =x(t) * h(t) \nonumber \\ & =\int_{-\infty}^{\infty} x(\tau) h(t-\tau) d \tau \label{eq_2_29} . \end{align} \]
The causality restriction on both signals and systems further simplifies the limits of integration in \(\eqref{eq_2_29}\). By definition, the response of a causal system cannot begin before its input begins. Consequently, the causal system's response to a unit impulse \(\delta(t)\) (which is located at \(t=0\) ) cannot begin before \(t=0\). Therefore, a causal system's unit impulse response \(h(t)\) is a causal signal.
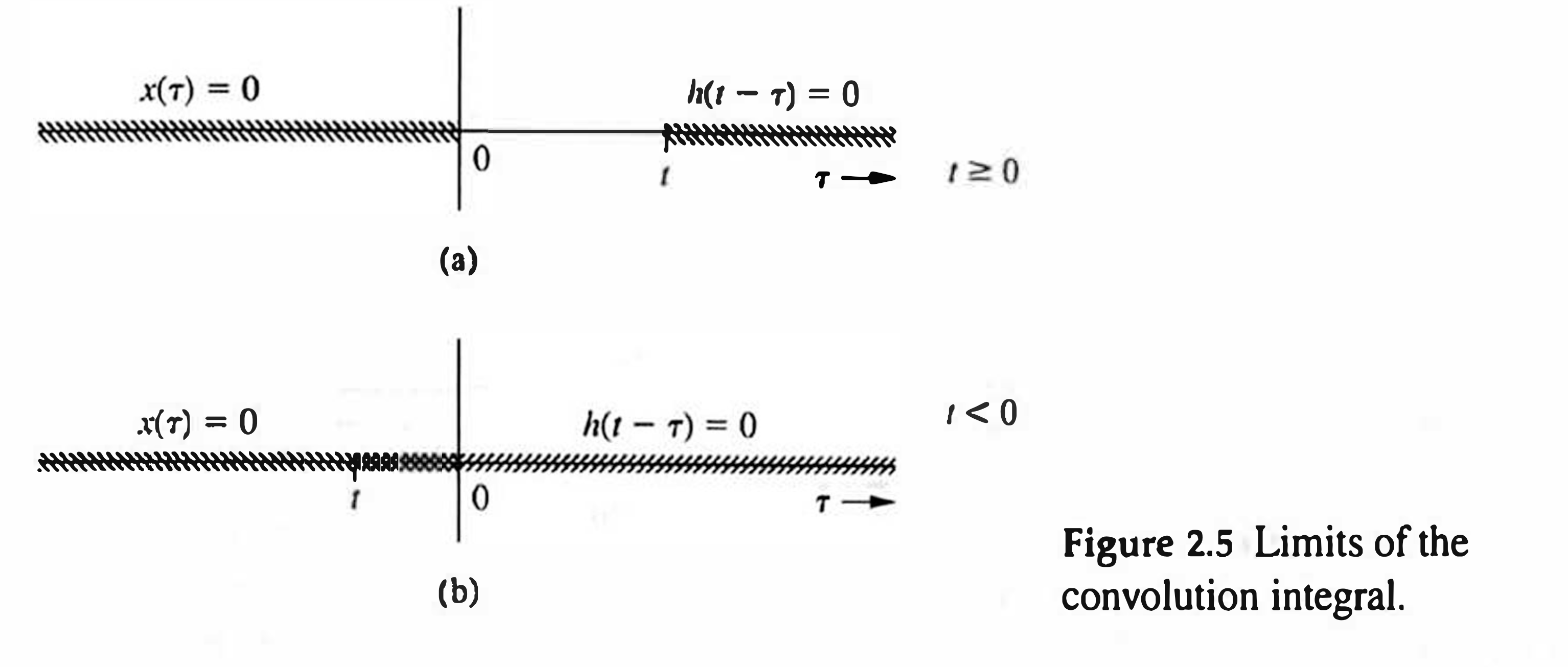
It is important to remember that the integration in \(\eqref{eq_2_29}\) is performed with respect to \(\tau\) (not \(t\) ). If the input \(x(t)\) is causal, \(x(\tau)=0\) for \(\tau<0\). Therefore, \(x(\tau)=0\) for \(\textcolor{pink} {\tau<0}\), as illustrated in Fig. 2.5a.
Similarly, if \(h(t)\) is causal, \(h(t-\tau)=0\) for \(t-\tau<0\); that is, for \(\textcolor{pink} {\tau>t}\), as depicted in Fig. 2.5a. Therefore, the product \(x(\tau) h(t-\tau)=0\) everywhere except over the nonshaded interval \(0 \leq \tau \leq t\) shown in Fig. 2.5a (assuming \(t \geq 0\) ).
Observe that if \(t\) is negative, \(x(\tau) h(t-\tau)=0\) for all \(\tau\), as shown in Fig. 2.5b.
Therefore, \(\eqref{eq_2_29}\) reduces to \[ y(t)=x(t) * h(t)= \begin{cases}\int_{0^{-}}^t x(\tau) h(t-\tau) d \tau & t \geq 0 \\ 0 & t<0\end{cases} \]
The lower limit of integration is taken as \(0^{-}\) to avoid the difficulty in integration that can arise if \(x(t)\) contains an impulse at the origin. This result shows that if \(x(t)\) and \(h(t)\) are both causal, the response \(y(t)\) is also causal.
Example: Computing the Zero-State Response
For an LTIC system with the unit impulse response \(h(t)=e^{-2 t} u(t)\), determine the response \(y(t)\) for the input \[ x(t)=e^{-t} u(t) \]
Solution:
Here, both \(x(t)\) and \(h(t)\) are causal (Fig. 2.6).
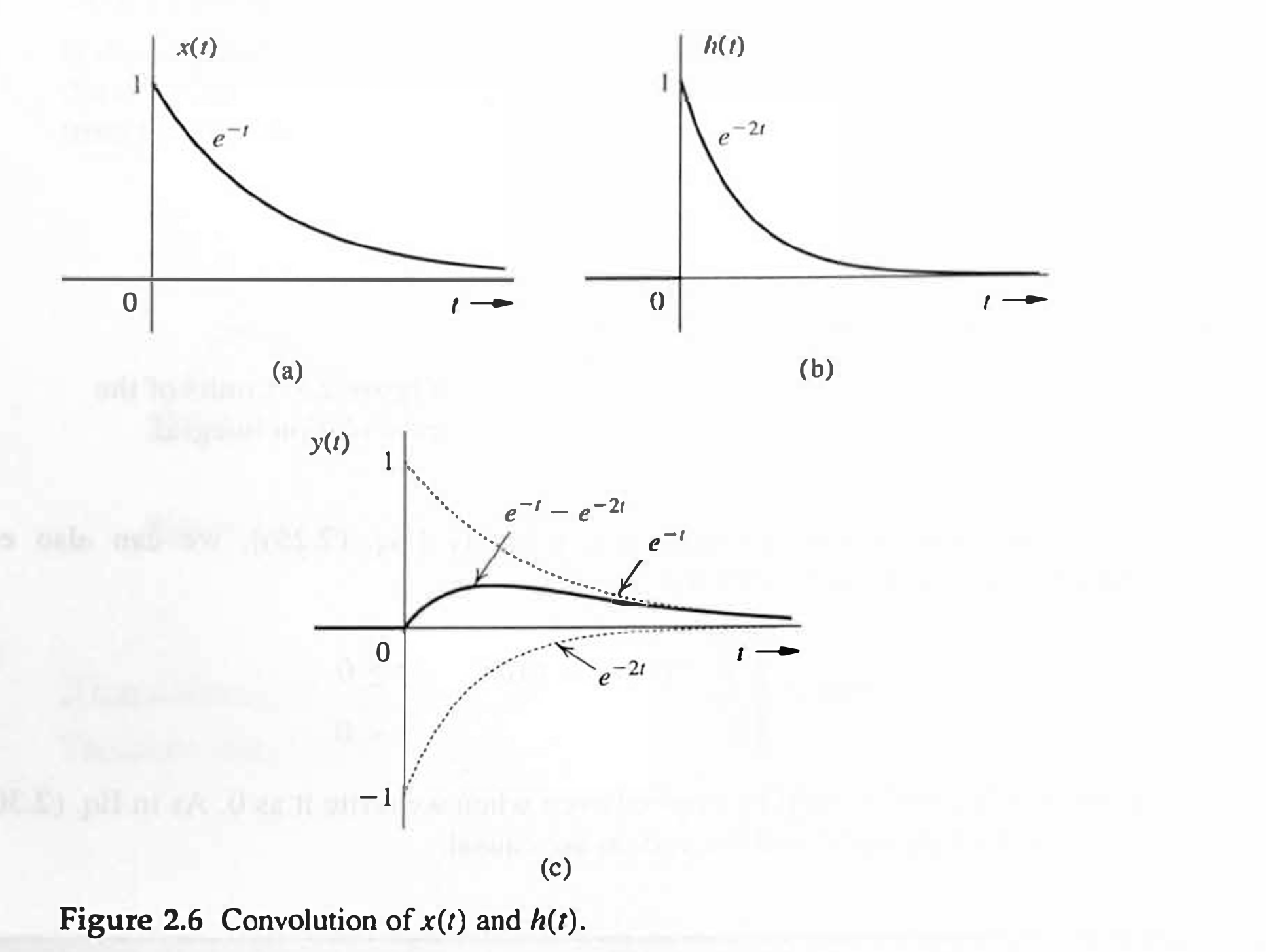
Hence, we obtain \[ y(t)=\int_0^t x(\tau) h(t-\tau) d \tau \quad t \geq 0 \]
Because \(x(t)=e^{-t} u(t)\) and \(h(t)=e^{-2 t} u(t)\), \[ x(\tau)=e^{-\tau} u(\tau) \quad \text { and } \quad h(t-\tau)=e^{-2(t-\tau)} u(t-\tau) \]
Remember that the integration is performed with respect to \(\tau\) (not \(t\) ), and the region of integration is \(0 \leq \tau \leq t\). Hence, \(\tau \geq 0\) and \(t-\tau \geq 0\). Therefore, \(u(\tau)=1\) and \(u(t-\tau)=1\); consequently, \[ y(t)=\int_0^t e^{-\tau} e^{-2(t-\tau)} d \tau \quad t \geq 0 \] Because this integration is with respect to \(\tau\), we can pull \(e^{-2 t}\) outside the integral, giving us \[ y(t)=e^{-2 t} \int_0^t e^\tau d \tau=e^{-2 t}\left(e^t-1\right)=e^{-t}-e^{-2 t} \quad t \geq 0 \]
Moreover, \(y(t)=0\) when \(t<0\) [see Eq. (2.30)]. Therefore, \[ y(t)=\left(e^{-t}-e^{-2 t}\right) u(t) \]
The response is depicted in Fig. 2.6c.
Interconnected systems
By its definition, the response of unit impulse \(\delta (t)\) is denoted as \(h(t)\), i.e., must be denotated with symbol \(h\).↩︎