Even and Odd Functions
Sources:
- B. P. Lathi & Roger Green. (2021). Chapter 1: Signals and Systems. Signal Processing and Linear Systems (2nd ed., pp. 64-136). Oxford University Press.
Even and odd functions
A function \(x_e(t)\) is said to be an even function of \(t\) if it is symmetrical about the vertical axis.
A function \(x_o(t)\) is said to be an odd function of \(t\) if it is antisymmetrical about the vertical axis.
Mathematically expressed, these symmetry conditions require \[ \begin{equation} \label{eq_1.15} x_e(t)=x_e(-t) \quad \text { and } \quad x_o(t)=-x_o(-t) \end{equation} \]
where e stands for even, o stands for odd.
An even function has the same value at the instants \(t\) and \(-t\) for all values of \(t\). On the other hand, the value of an odd function at the instant \(t\) is the negative of its value at the instant \(-t\). An example even signal and an example odd signal are shown in Figs. 1.23a and 1.23b, respectively.
Even and odd components of a signal
Every signal \(x(t)\) can be expressed as a sum of even and odd components because \[ \begin{equation} \label{eq_1.17} x(t)=\underbrace{\frac{1}{2}[x(t)+x(-t)]}_{\text {even }}+\underbrace{\frac{1}{2}[x(t)-x(-t)]}_{\text {odd }} \end{equation} \]
From the definitions in \(\eqref{eq_1.15}\) , we can clearly see that the first component on the right-hand side is an even function, while the second component is odd.
Finding the even and odd components of a signal
Given a signal \(x(t)=e^{-a t} u(t)\), based on \(\eqref{eq_1.17}\), we can expressas a sum of the even component \(x_e(t)\) and the odd component \(x_o(t)\) as \[ x(t)=x_e(t)+x_o(t) \] where \[ x_e(t)=\frac{1}{2}\left[e^{-a t} u(t)+e^{a t} u(-t)\right] \quad \text { and } \quad x_o(t)=\frac{1}{2}\left[e^{-a t} u(t)-e^{a t} u(-t)\right] \]
The function \(e^{-a t} u(t)\) and its even and odd components are illustrated in Fig. 1.24.
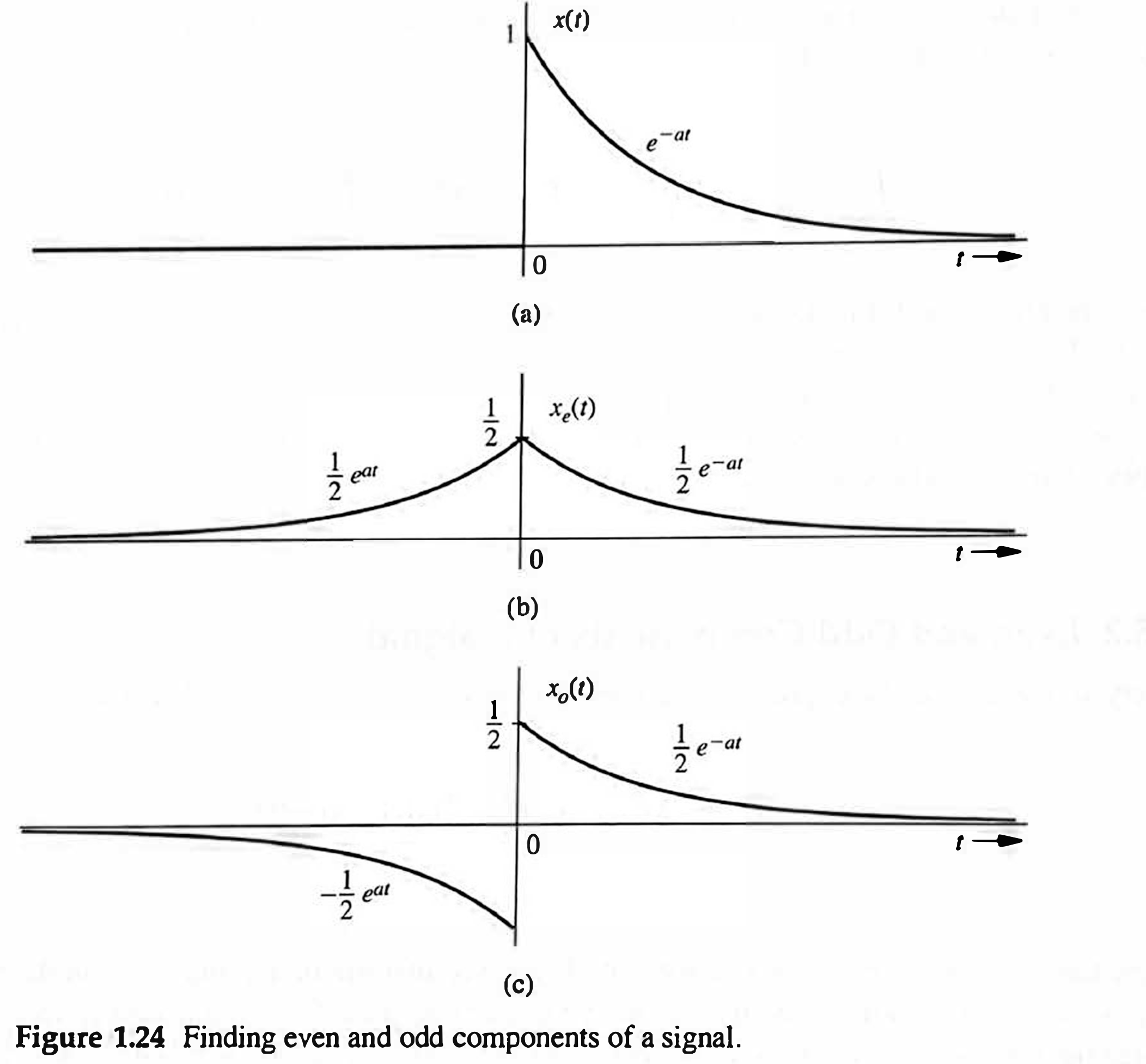
A Modification for complex signals
While a complex signal can be decomposed into even and odd components, it is more common to decompose complex signals using conjugate symmetries.
- A complex signal \(x(t)\) is said to be conjugate-symmetric if \(x(t)=x^*(-t)\).
- A conjugate-symmetric signal is even in the real part and odd in the imaginary part. Thus, a real conjugate-symmetric signal is an even signal.
- A signal is conjugate-antisymmetric if \(x(t)=-x^*(-t)\).
- A conjugate-antisymmetric signal is odd in the real part and even in the imaginary part. A real conjugate-antisymmetric signal is an odd signal.
Any signal \(x(t)\) can be decomposed into a conjugate-symmetric portion \(x_{c s}(t)\) plus a conjugate-antisymmetric portion \(x_{c a}(t)\). That is, \[ x(t)=x_{c s}(t)+x_{c a}(t) \] where \[ x_{c s}(t)=\frac{x(t)+x^*(-t)}{2} \quad \text { and } \quad x_{c a}(t)=\frac{x(t)-x^*(-t)}{2} \]
The proof is similar to the one for decomposing a signal into even and odd components. As we shall see in later chapters, conjugate symmetries commonly occur in real-world signals and their transforms.