The Vector Quantised-Variational AutoEncoder (VQ-VAE), differs from VAEs in two key ways: the encoder network outputs discrete, rather than continuous, codes; and the prior is learnt rather than static.
In VQ-VAE, we have:
An input image \(x \in \mathbb{R}^{H \times W \times 3}\) where \(H, W\) are the height and width of the image.
A latent embedding space \(\mathcal{E}=\left\{e_k\right\}_{k=1}^K \subset \mathbb{R}^{D}\), called the codebook, where each \(e_k\) is called a code and \(D\) is the dimensionality of codes.
An encoder\[
\begin{align}
& \operatorname{E} : \mathbb{R}^{H \times W \times 3} \rightarrow \mathbb{R}^{h \times w \times D} \label{eq_encoder_1}
\\
& \operatorname{E}(x) = z_e \label{eq_encoder_2}
\end{align}
\] encodes an image \(x\) into an embedding \(z_e\).
An operator called quantizer: \[
\begin{aligned}
& \operatorname{Qtzr} : \mathbb{R}^{h \times w \times D} \rightarrow \mathbb{R}^{h \times w \times D} \\
& \operatorname{Qtzr}(z_e) = z_q ,
\end{aligned}
\]
quantizes \(z_e\) to \(z_q\), where \(z_q, z_e \in \mathbb{R}^{h \times w \times D}\). The quantization process is \[
z_{q_{ij}} = {\arg\min} \|z_{e_{ij}} - e_k\|
\] with subscript \(i, j\) starting from \(1\) to $ h, w$.
Therefore, for each element \(z_{e_{i j}}\) of \(z_e\), we use argmin to find the \(e_k\) that is closest in distance to \(z_{e_{i j}}\), i.e., minimizing the norm \(\left\|z_{e_{i j}}-e_k\right\|\), to get \(z_{q_{i,j}}\).
A decoder\[
\begin{align}
& \operatorname{D} : \mathbb{R}^{h \times w \times D} \rightarrow \mathbb{R}^{H \times W \times 3} \label{eq_decoder_1}
\\
& \operatorname{D}(z_q) = \hat x \label{eq_decoder_2}
\end{align}
\] decodes \(z_q\) into an image \(\hat x\), which is also called the reconstructed image of \(x\).
Forward pass
VQ-VAE
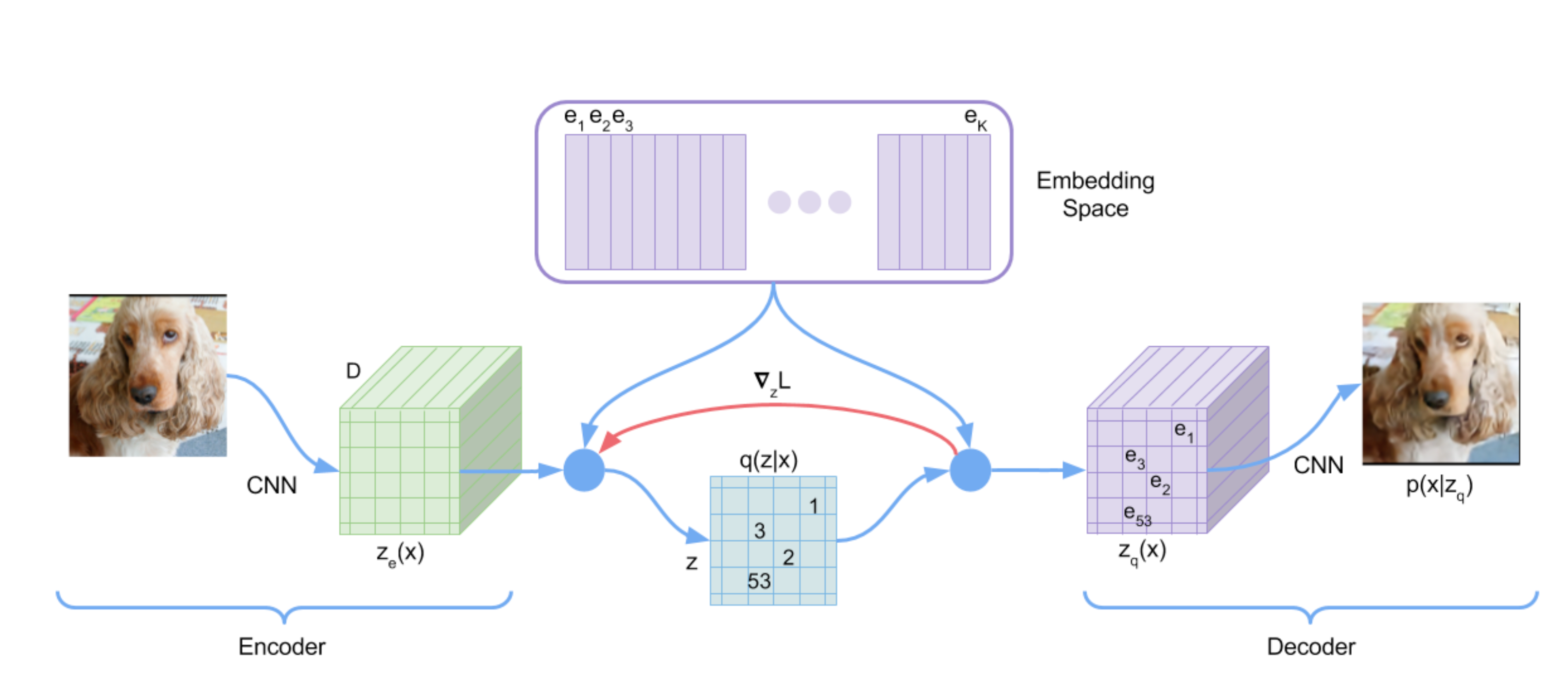
The forward pass of VQ-VAE consists of
First, we use encoder \(\operatorname{E(.)}\) to encode the input image \(x\) to get the embedding \(z_e\): \[
z_e = \operatorname{E}(x) .
\]
Next, we use quantizer \(\operatorname{Qtzr}(.)\) to quantize the embedding \(z_e\) to get the quantized embedding \(z_q\). Since \(z_e\) contains \(h\times w\) embeddings, \(z_q\) is composed of \(h \times w\) codes, of which each code \(e_k\) is selected through a nearest-neighbor lookup (argmin()) to the codebook \(\mathcal{E}=\left\{e_k\right\}_{k=1}^K\).
Finnally, we use decoder to decode \(z_e\) to get the reconstructed image \(\hat x\).
NOTES:
The encoded embedding \(z_e\) and quantized embedding \(z_q\) have the same dimentionality \[
z_e, z_q \in \mathbb{R}^{h \times w \times D} .
\] and they have the same embedding dimenstion (=\(D\)) as \(e_k\).
We will sometimes use \(z_e(x), z_q(x)\) to refer \(z_e, z_q\).
Loss function
The overall loss function is: \[
L=
\color{blue} {-\log p\left(x \mid z_q\right)} +
\color{green} {\left\|\operatorname{sg}(z_e -z_q) \right\|_2^2} +
\color{purple}{\beta\left\|z_e -\operatorname{sg}(z_q)\right\|_2^2},
\] Since VQ-VAE leverages argmin() function, which is non-differentiable. The gradient \(\nabla_{z_q} L\) from decoder input \({z}_q\) can not be passed to the encoder output \(\mathbf{z}_e\). To solve this, we use a trick called the straight through estimator which applies a stop_gradient operator (\(\operatorname{sg}\) in the equation) to copy\(\nabla_{z_q} L\) to \(z_e\).
The overall loss function has three components:
Reconstruction loss \(\color{blue} {-\log p\left(x \mid z_q\right)}\) is the negative log-likelihood. In practice, it's common to replace it with MSE loss.
Codebook loss \(\color{green} {\left\|\operatorname{sg}\left[z_e(x)\right]-e\right\|_2^2}\), which moves the embedding vectors towards the encoder output.
Commitment loss \(\color{purple}{\beta\left\|z_e(x)-\operatorname{sg}[e]\right\|_2^2}\), which encourages the encoder output to stay close to the embedding space.
Model architecture
#TODO shape problem
VectorQuantizer
This layer takes a tensor to be quantized. The channel dimension will be used as the space in which to quantize. All other dimensions will be flattened and will be seen as different examples to quantize.
The output tensor will have the same shape as the input.
As an example for a BCHW tensor of shape [16, 64, 32, 32], we will first convert it to an BHWC tensor of shape [16, 32, 32, 64] and then reshape it into [16384, 64] and all 16384 vectors of size 64 will be quantized independently. In otherwords, the channels are used as the space in which to quantize.
All other dimensions will be flattened and be seen as different examples to quantize, 16384 in this case.
We will also implement a slightly modified version which will use exponential moving averages to update the embedding vectors instead of an auxillary loss. This has the advantage that the embedding updates are independent of the choice of optimizer for the encoder, decoder and other parts of the architecture. For most experiments the EMA version trains faster than the non-EMA version.
defforward(self, inputs): # convert inputs from BCHW -> BHWC inputs = inputs.permute(0, 2, 3, 1).contiguous() # (256, 64, 8, 8) BCHW --> (256, 8, 8, 64) BHWC input_shape = inputs.shape # BHWC # Flatten input flat_input = inputs.view(-1, self._embedding_dim) # Now set C'=64 (_embedding_dim), flatten `inputs` into (N, C'), where N=B*H*W, i.e., we have N=B*H*W vectors, each vector has dimension=C. # Calculate distances distances = (torch.sum(flat_input**2, dim=1, keepdim=True) + torch.sum(self._embedding.weight**2, dim=1) - 2 * torch.matmul(flat_input, self._embedding.weight.t())) # Each vector `z_e` has distances with all the quantized vectors `e_j` in the codebook, where j in K = `_num_embeddings`. # Encoding encoding_indices = torch.argmin(distances, dim=1).unsqueeze(1)# For each vector `z_e`, select the index of the **closest** quantized vector `e_j` in the codebook. # For each each vector `z_e`, use the index of its corresponding `z_q` to create a one-hot encoding. encodings = torch.zeros(encoding_indices.shape[0], self._num_embeddings, device=inputs.device) encodings.scatter_(1, encoding_indices, 1) # Quantize and unflatten quantized = torch.matmul(encodings, self._embedding.weight).view(input_shape) # Use the one-hot encoding as the index to select the quantized vectors in the codebook. # Use EMA to update the embedding vectors if self.training: self._ema_cluster_size = self._ema_cluster_size * self._decay + \ (1 - self._decay) * torch.sum(encodings, 0) # Laplace smoothing of the cluster size n = torch.sum(self._ema_cluster_size.data) self._ema_cluster_size = ( (self._ema_cluster_size + self._epsilon) / (n + self._num_embeddings * self._epsilon) * n) dw = torch.matmul(encodings.t(), flat_input) self._ema_w = nn.Parameter(self._ema_w * self._decay + (1 - self._decay) * dw) self._embedding.weight = nn.Parameter(self._ema_w / self._ema_cluster_size.unsqueeze(1)) # Loss e_latent_loss = F.mse_loss(quantized.detach(), inputs) commitment_loss = self._commitment_cost * e_latent_loss codebook_loss = F.mse_loss(quantized, inputs.detach()) # Straight Through Estimator quantized = inputs + (quantized - inputs).detach() avg_probs = torch.mean(encodings, dim=0) perplexity = torch.exp(-torch.sum(avg_probs * torch.log(avg_probs + 1e-10))) # convert quantized from BHWC -> BCHW return codebook_loss, commitment_loss, quantized.permute(0, 3, 1, 2).contiguous(), perplexity, encodings
