Bellman Equation: The Matrix-Vector Form
Sources:
- Shiyu Zhao. Chapter 2: State Values and Bellman Equation. Mathematical Foundations of Reinforcement Learning.
- --> Youtube: Bellman Equation: Matrix-Vector form
Bellman equation: the matrix-vector form
Consider the Bellman equation:
It's an elementsise form. That means there are
Recall that this equation can be rewritten as
Suppose the states could be indexed as
Put all these equations for all the states together and rewrite to a matrix-vector form
Examples
Refer to the grid world example for the notations.
If there are four states,
For deterministic policy
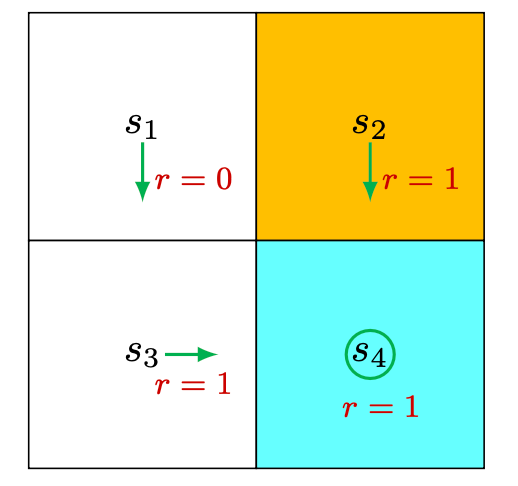
For this specific example:
For stochastic policy
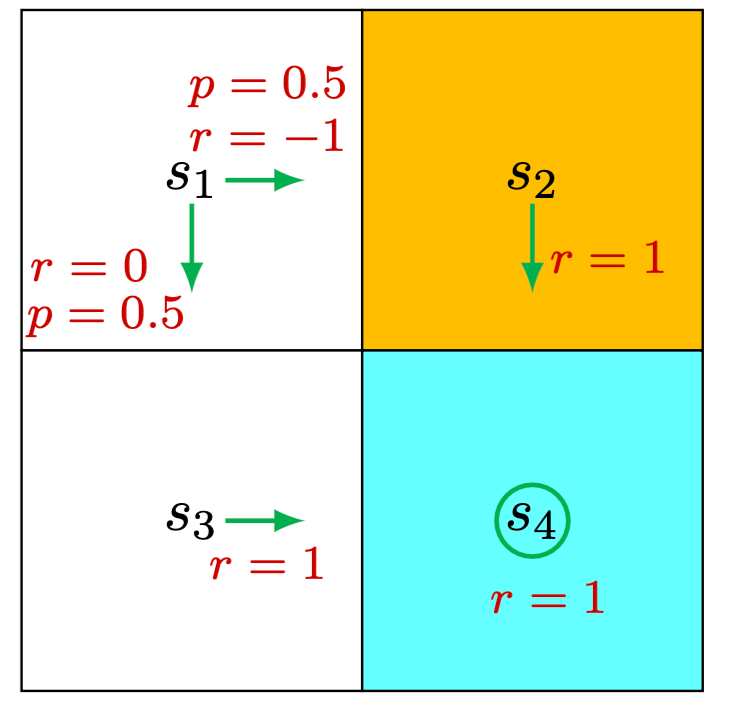
For this specific example:
Solution of the matrix-vector form
Recalling the Bellman equation in matrix-vector form
We can convert it to two forms:
The closed-form solution is:
An iterative solution is:
We can just randomly select a matrix
Proof: the closed-form solution
First, the Bellman equation in matrix-vector form is
Now we calculate the matrix inverse:
Proof: the iterative solution
Define the error as
into
As a result,
Note that