Common Loss Functions

• Cross entropy
• Focal loss
• Hinge loss
• ...

Notations

TO make the context clear, in this article, we make the following regulations:

• The size of the dataset, i.e., the number of the datapoints, is denoted as $N$.
• The datapoint of index $i$ is $x_i\in {\mathbb{R}}^{d\times 1}$. The last dimenstion of it is denoted as $y_i\in {\mathbb{R}}^{1\times 1}$.
• The predicted datapoint by the model is, corresponding to $x_i$, is ${\hat{x}}_i$. The last dimenstion of it is ${\hat{y}}_i$.
• The predicted value of the $i^{\text{th}}$ datapoint output by the model is $p_i$.
• When the task is a classification task, the ground truth value is often a 0/1 label, i.e., $y_i\in \{0,1\},\mathrm{\forall }i$.
• When the task is a classification task, the number of classes is $C$. In addition, the ground truth label value and the prediction value of $c^{\text{th}}$ class of the $i^{\text{th}}$ datapoint is $y_c,p_c$.

Mean Squared Error

Mean squared error (MSE) loss is $$\mathrm{MSE}\mathrm{Loss}=\Vert y_i-{\hat{y}}_i{\Vert }_2^2=\sqrt{\sum _{i=1}^n{(y_i-{\hat{y}}_i)}^2}.$$

import torch

def mse(y_true, y_predicted):
    # Mean Squared Error (MSE) between x and y
    mse = torch.mean((y_true - y_predicted) ** 2)
    print("Mean Squared Error between y and \hat y:", mse.item())

Cross Entropy

For the gradient (or derivation) of Cross Entropy, please refer to ->this article.

--> Youtube: Cross Entropy

Cross-entropy loss (often abbreviated as CE), or log loss, measures the performance of a classification model whose output is a probability value between 0 and 1 (usually produced by a softmax function).

The cross entropy loss $L$ of a sample is $$L=-\sum _{i=1}^C{y}_i\log \left({\hat{y}}_i\right).$$

where ${\hat{y}}_i$ is the predicted probability for class $i$, usually obtained by applying the softmax function to the logits For classification tasks where there is only one true class for a sample, i.e., $y_c\in \{0,0,\cdots ,1,0,\cdots \}$, suppose the index of the true class of the input data point is $t$, we obtain $$L=-(0+\cdots +0+1\cdot \log ({\hat{y}}_t)+0+\cdots +0)=-\log ({\hat{y}}_t)$$

import torch

def calculate_cross_entropy(y_true, y_predicted):
    '''
    :param y_predicted: The predicted, often by model, distribution of data point y.
    :param y_true: The true distribution of data point y.
    :return: the cross entropy of p_predicted, given the fact that the true distribution is y_true.
    Note: y_predicted and y_true are  multi-variance distributions if X is multidimensional.
    '''
    # Ensure that p_predict and y_true have the same length
    if y_predicted.shape != y_true.shape:
        raise ValueError("Tensors p_predict and y_true must have the same shape")

    # Avoid log(0) situation
    epsilon = 1e-15
    # Clamps all elements of p_predicted in input into the range [ min, max ] where min =epsilon, and max = 1 - epsilon.
    y_predicted = torch.clamp(y_predicted, epsilon, 1 - epsilon)

    # Calculate cross entropy
    cross_entropy = -torch.sum(y_true * torch.log(y_predicted))
    return cross_entropy

Example

For example, consider following neural network, there're three data points "Setosa", "Virginica" and "Versicolor", each is a 2-D vector. The number of classes is $N=3$ since softmax outputs 3 values.

Example of NN with softmax

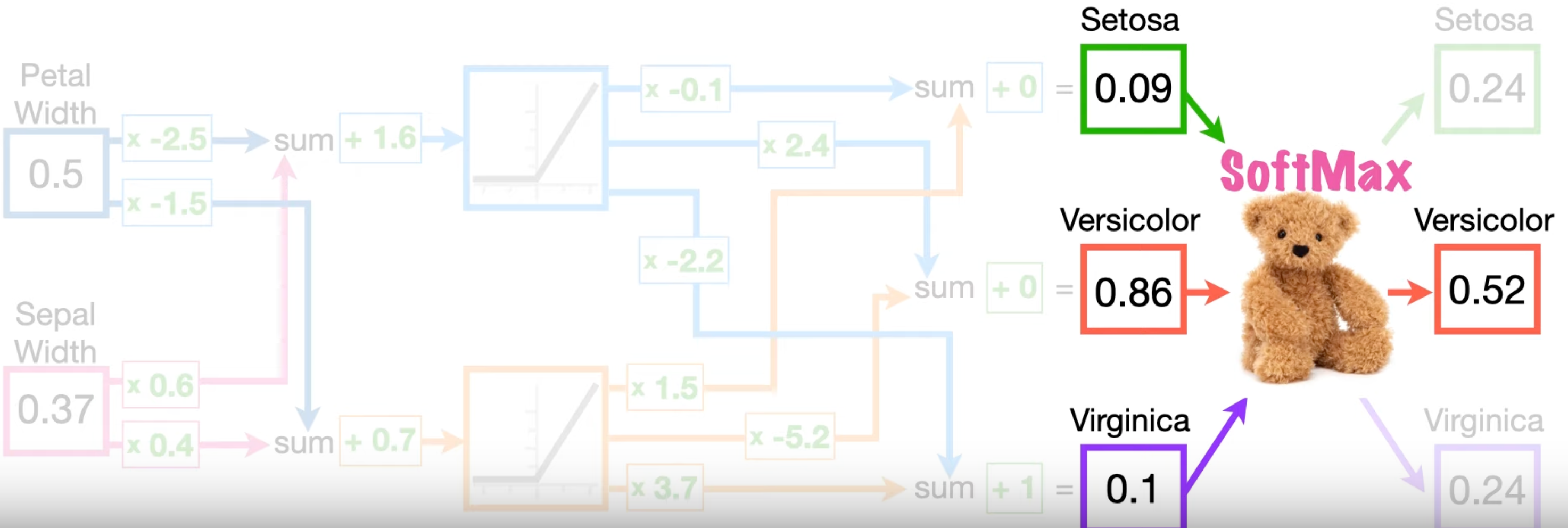
Petal	Sepal	Species	$p$	Cross Entropy
0.04	0.42	Setosa	0.57	$1.(-\log (p))+0+0=0.56$
1	0.54	Virginica	0.58	$0+1.-(p)+0=0.54$
0.50	0.37	Versicolor	0.52	$0+0+-\log (p)=0.65$

Take Sepal for Versicolor, when input is Versicolor ($[0.50,0.37]$), the true label value of Versicolor is $1$ and that of others is all $0$. $$\begin{array}{r}{y}_{\text{Setosa}}=0,\\ y_{\text{Virginica}}=0,\\ y_{\text{Versicolor}}=1,\end{array}$$ The output of softmax corresponding to Versicolor is $p_{\text{Versicolor}}=0.52$.

Therefore, the cross entropy of this training is $$1.(-\log (p))+0+0=0.56.$$

Property

CE loss vs. model prediction

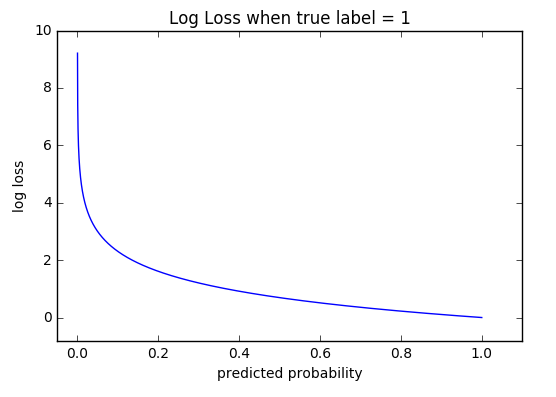
The graph above shows the range of possible loss values given a true observation (isDog = 1). As the predicted probability approaches 1, log loss slowly decreases. As the predicted probability decreases, however, the log loss increases rapidly.

Log loss heavily penalizes those predictions that are confident and wrong.

Problems

The main problem of cross entropy is that, even when the prediction is correct, i.e., y_predicted == y_true, the cross entropy isn't symmetric.

A Problem of Cross Entropy

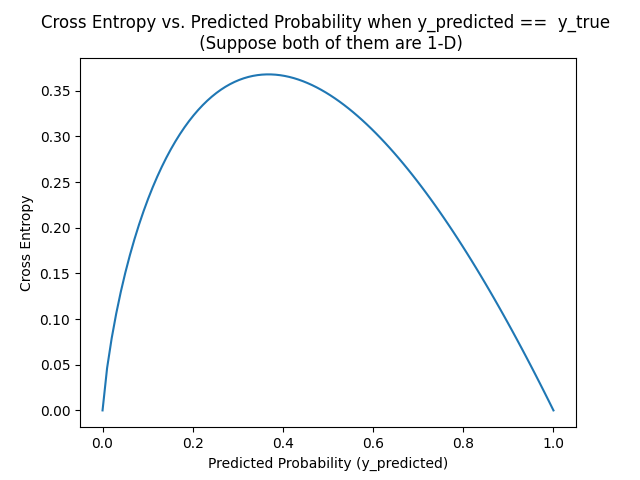
From this figure, if y_predicted == y_true == 0.2, their CE is 0.3218.... If y_predicted == y_true == 0.8, their CE is 0.178514. They're not equal!

Focal Loss

--> Focal Loss for Dense Object Detection

A Focal Loss function addresses (extreme) class imbalance during training in tasks like object detection. Focal loss applies a modulating term to the cross entropy loss in order to focus learning on hard misclassified examples.

Formally, the Focal Loss adds a factor ${(1-{\hat{y}}_t)}^{\gamma }$ to the standard cross entropy criterion. $$\mathrm{FL}\left({\hat{y}}_t\right)=-{(1-{\hat{y}}_t)}^{\gamma }\log \left({\hat{y}}_t\right)$$

Property

(In the below figure, the notation $\hat{y}$ is replaced by $p$)

FL loss vs. model prediction

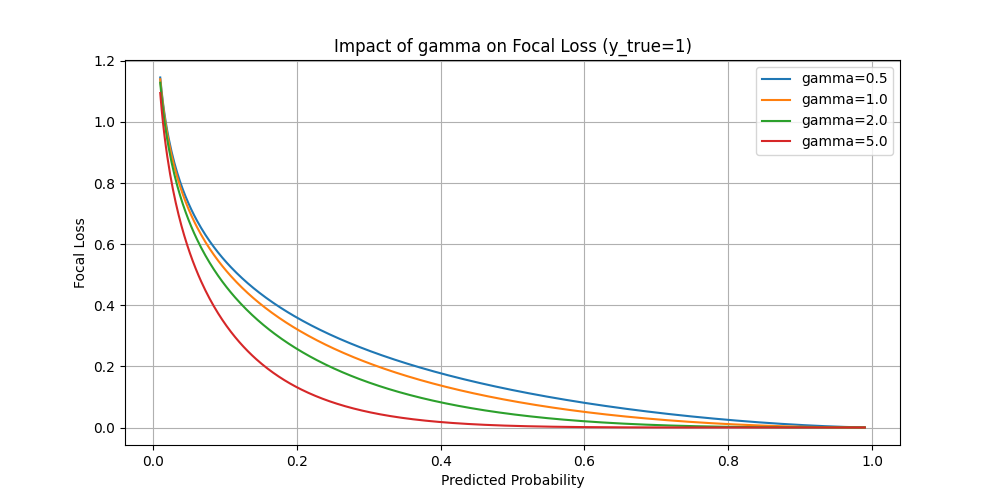
• Setting $\gamma >0$ reduces the relative loss for well-classified examples $({\hat{y}}_t>.5)$, putting more focus on hard, misclassified examples. Here there is tunable focusing parameter $\gamma \ge 0$.
• One typical use case is in object detection tasks. An image may contain 5 onjects whereas the the number of bounding boxes can be millions. Thus there're enormous negative datapoints. The model can easily learn to judge all data points to be false to achieve a high traing performance.

import torch

def focal_loss(y_true, y_predicted, alpha=0.25, gamma=2.0):
    # First calculate the cross entropy loss using the helper function
    ce_loss = calculate_cross_entropy(y_true, y_predicted)

    # Calculate p_t
    p_t = y_true * y_predicted + (1 - y_true) * (1 - y_predicted)

    # Calculate the modulating factor
    modulating_factor = (1 - p_t) ** gamma

    # Apply the alpha weighting
    alpha_factor = y_true * alpha + (1 - y_true) * (1 - alpha)

    # Calculate the final Focal Loss
    focal_loss = alpha_factor * modulating_factor * ce_loss
    return focal_loss

Dice Loss

--> Source

Dice Loss was originally designed for binary classification problems, particularly in the context of binary segmentation where you're often distinguishing between the foreground and the background.

Dice Coefficient

It's derived from Dice Coefficient, which is a statistic used to gauge the similarity of two samples.

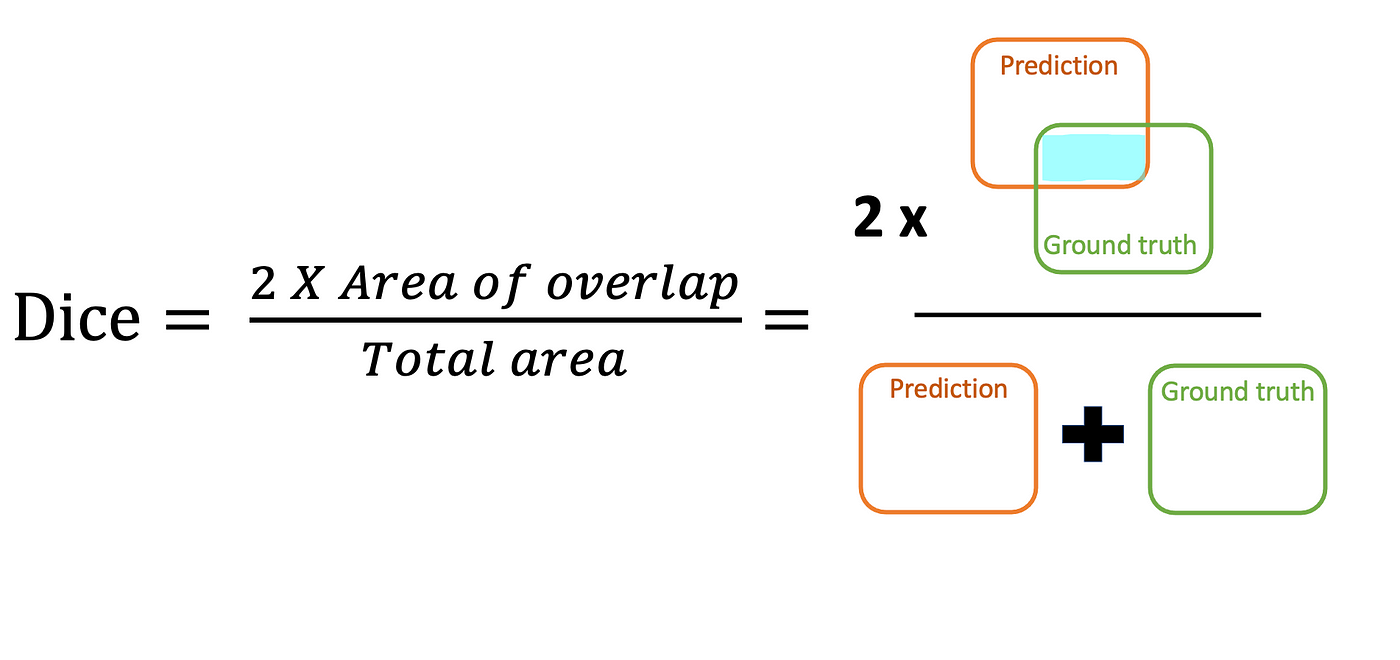For the $i^{\text{th}}$ datapoint, the Dice Coefficient is $$\mathrm{Dice}=\frac{2\times \sum _i({\hat{y}}_i\times y_i)}{\sum _i{\hat{y}}_i+\sum _i{y}_i}.$$

def dice_coef(groundtruth_mask, pred_mask):
    intersect = np.sum(pred_mask*groundtruth_mask)
    total_sum = np.sum(pred_mask) + np.sum(groundtruth_mask)
    dice = np.mean(2*intersect/total_sum)
    return round(dice, 3) #round up to 3 decimal places

Dice Loss

The Dice Loss is $$\mathrm{DL}=1-\mathrm{Dice}.$$

def dice_loss(groundtruth_mask, pred_mask):
	return 1 - dice_coef(groundtruth_mask, pred_mask)

IoU

--> Source

img

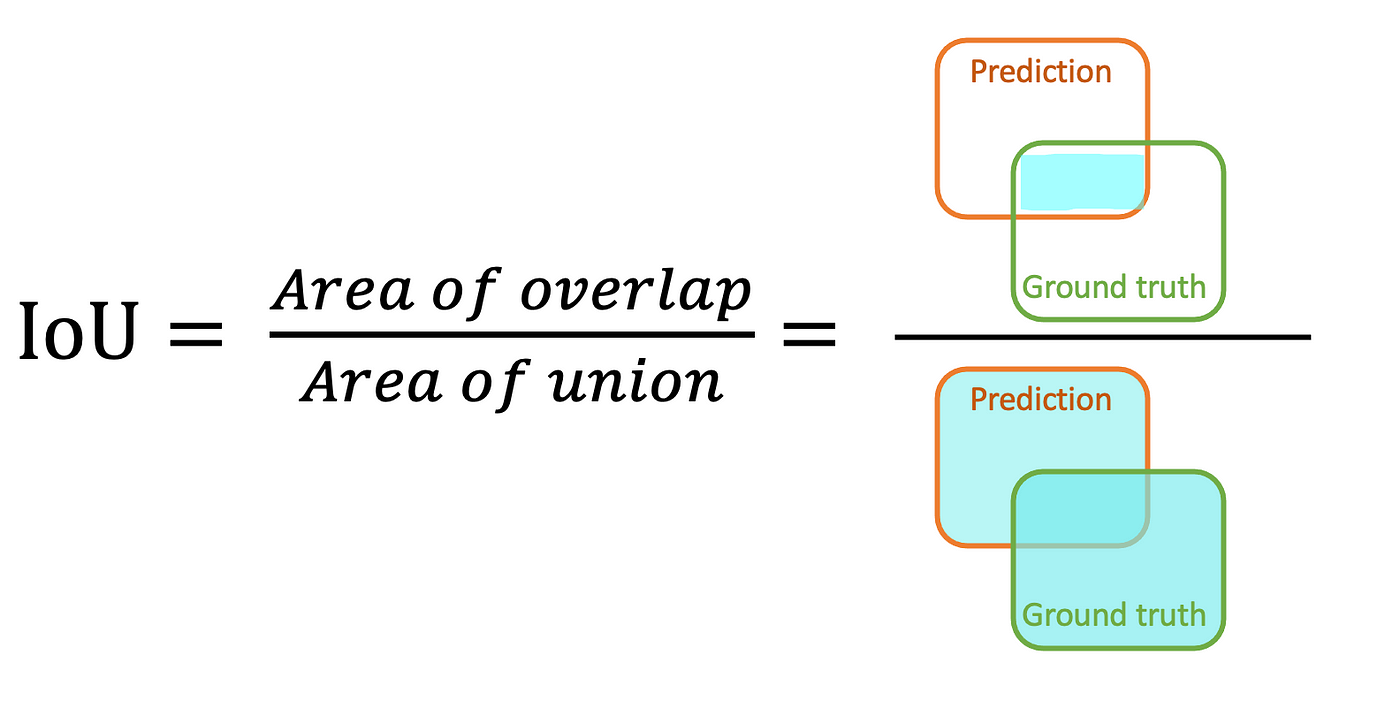
Jaccard index, also known as Intersection over Union (IoU), is the area of the intersection over union of the predicted segmentation and the ground truth $$\mathrm{I}\mathrm{o}\mathrm{U}=\frac{TP}{TP+FP+FN}$$

def iou(groundtruth_mask, pred_mask):
    intersect = np.sum(pred_mask*groundtruth_mask)
    union = np.sum(pred_mask) + np.sum(groundtruth_mask) - intersect
    iou = np.mean(intersect/union)
    return round(iou, 3)