Bellman Equation: The Matrix-Vector Form
Sources:
- Shiyu Zhao. Chapter 2: State Values and Bellman Equation. Mathematical Foundations of Reinforcement Learning.
- --> Youtube: Bellman Equation: Matrix-Vector form
Bellman equation: the matrix-vector form
Consider the Bellman equation: \[ v_\pi(s)=\sum_a \pi(a \mid s)\left[\sum_r p(r \mid s, a) r+\gamma \sum_{s^{\prime}} p\left(s^{\prime} \mid s, a\right) v_\pi\left(s^{\prime}\right)\right] \]
It's an elementsise form. That means there are \(|\mathcal{S}|\) equations like this! If we put all the equations together, we have a set of linear equations, which can be concisely written in a matrix-vector form.
Recall that this equation can be rewritten as \[ v_\pi(s)= \color{teal}{r_\pi(s)} + \gamma \color{salmon}{\sum_{s^{\prime}} p_\pi\left(s^{\prime} \mid s\right) v_\pi\left(s^{\prime}\right)} \] where \[ r_\pi(s) \triangleq \sum_a \pi(a \mid s) \sum_r p(r \mid s, a) r, \quad p_\pi\left(s^{\prime} \mid s\right) \triangleq \sum_a \pi(a \mid s) p\left(s^{\prime} \mid s, a\right) \]
Suppose the states could be indexed as \(s_i(i=1, \ldots, n)\). For state \(s_i\), the Bellman equation is \[ v_\pi\left(s_i\right)= \color{teal}{r_\pi\left(s_i\right)}+ \gamma \color{salmon} {\sum_{s_j} p_\pi\left(s_j \mid s_i\right) v_\pi\left(s_j\right)} \]
Put all these equations for all the states together and rewrite to a matrix-vector form \[ \begin{equation} \label{eq_Bellman_equation_matrix-vector_form} v_\pi= \color{teal}{r_\pi} + \gamma \color{salmon}{P_\pi v_\pi} \end{equation} \] where
\(v_\pi=\left[v_\pi\left(s_1\right), \ldots, v_\pi\left(s_n\right)\right]^T \in \mathbb{R}^n\),
\(r_\pi=\left[r_\pi\left(s_1\right), \ldots, r_\pi\left(s_n\right)\right]^T \in \mathbb{R}^n\),
\(P_\pi \in \mathbb{R}^{n \times n}\), where \(\left[P_\pi\right]_{i j}=p_\pi\left(s_j \mid s_i\right)\), is the state transition matrix.
Examples
Refer to the grid world example for the notations.
If there are four states, \(v_\pi=r_\pi+\gamma P_\pi v_\pi\) can be written out as \[ \underbrace{\left[\begin{array}{l} v_\pi\left(s_1\right) \\ v_\pi\left(s_2\right) \\ v_\pi\left(s_3\right) \\ v_\pi\left(s_4\right) \end{array}\right]}_{v_\pi}=\underbrace{\left[\begin{array}{l} r_\pi\left(s_1\right) \\ r_\pi\left(s_2\right) \\ r_\pi\left(s_3\right) \\ r_\pi\left(s_4\right) \end{array}\right]}_{r_\pi}+\gamma \underbrace{\left[\begin{array}{llll} p_\pi\left(s_1 \mid s_1\right) & p_\pi\left(s_2 \mid s_1\right) & p_\pi\left(s_3 \mid s_1\right) & p_\pi\left(s_4 \mid s_1\right) \\ p_\pi\left(s_1 \mid s_2\right) & p_\pi\left(s_2 \mid s_2\right) & p_\pi\left(s_3 \mid s_2\right) & p_\pi\left(s_4 \mid s_2\right) \\ p_\pi\left(s_1 \mid s_3\right) & p_\pi\left(s_2 \mid s_3\right) & p_\pi\left(s_3 \mid s_3\right) & p_\pi\left(s_4 \mid s_3\right) \\ p_\pi\left(s_1 \mid s_4\right) & p_\pi\left(s_2 \mid s_4\right) & p_\pi\left(s_3 \mid s_4\right) & p_\pi\left(s_4 \mid s_4\right) \end{array}\right]}_{P_\pi} \underbrace{\left[\begin{array}{l} v_\pi\left(s_1\right) \\ v_\pi\left(s_2\right) \\ v_\pi\left(s_3\right) \\ v_\pi\left(s_4\right) \end{array}\right]}_{v_\pi} . \]
For deterministic policy
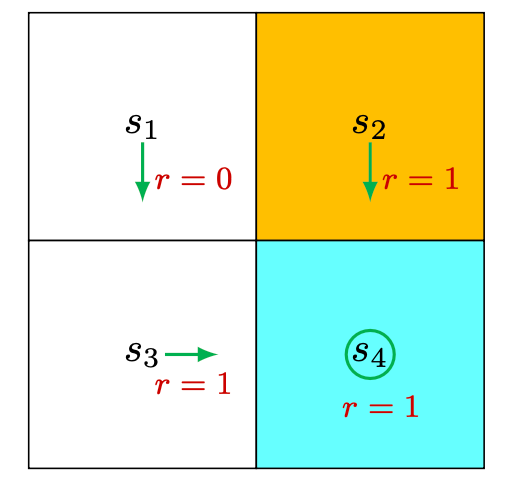
For this specific example: \[ \left[\begin{array}{l} v_\pi\left(s_1\right) \\ v_\pi\left(s_2\right) \\ v_\pi\left(s_3\right) \\ v_\pi\left(s_4\right) \end{array}\right]=\left[\begin{array}{l} 0 \\ 1 \\ 1 \\ 1 \end{array}\right]+\gamma\left[\begin{array}{llll} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 \end{array}\right]\left[\begin{array}{l} v_\pi\left(s_1\right) \\ v_\pi\left(s_2\right) \\ v_\pi\left(s_3\right) \\ v_\pi\left(s_4\right) \end{array}\right] \]
For stochastic policy
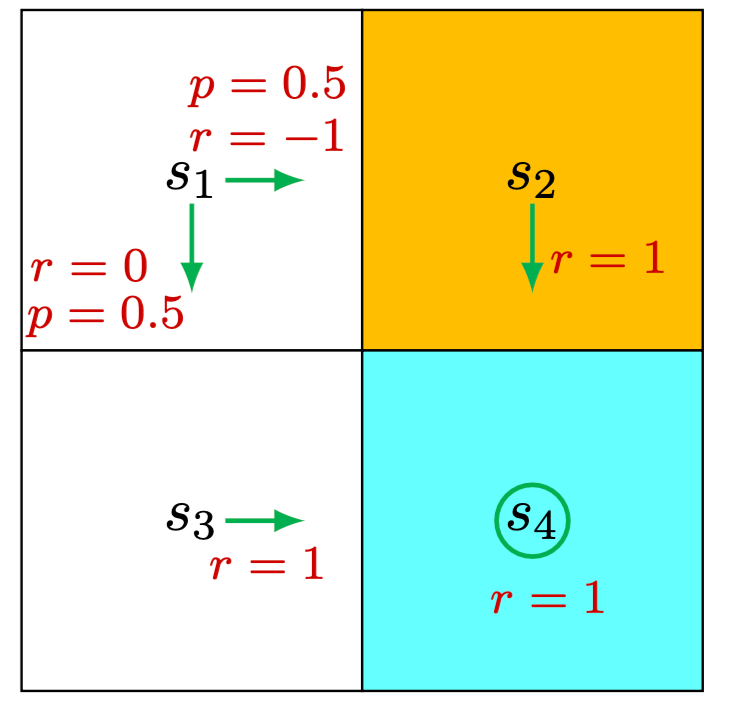
For this specific example: \[ \left[\begin{array}{c} v_\pi\left(s_1\right) \\ v_\pi\left(s_2\right) \\ v_\pi\left(s_3\right) \\ v_\pi\left(s_4\right) \end{array}\right]=\left[\begin{array}{c} 0.5(0)+0.5(-1) \\ 1 \\ 1 \\ 1 \end{array}\right]+\gamma\left[\begin{array}{cccc} 0 & 0.5 & 0.5 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 \end{array}\right]\left[\begin{array}{l} v_\pi\left(s_1\right) \\ v_\pi\left(s_2\right) \\ v_\pi\left(s_3\right) \\ v_\pi\left(s_4\right) \end{array}\right] \]
Solution of the matrix-vector form
Recalling the Bellman equation in matrix-vector form \(\eqref{eq_Bellman_equation_matrix-vector_form}\),
We can convert it to two forms:
The closed-form solution is: \[ v_\pi=\left(I-\gamma P_\pi\right)^{-1} r_\pi \] The drawback of closed-form solution is that it involves a matrix inverse operation, which is computationally expensive. Thus, in practice, we'll use an iterative solution.
An iterative solution is: \[ v_{k+1}=r_\pi+\gamma P_\pi v_k , \] where \(I\) is the identity matrix.
We can just randomly select a matrix \(v_0\), then calculate \(v_1, v_2, \cdots\). This leads to a sequence \(\left\{v_0, v_1, v_2, \ldots\right\}\). We can show that \[ v_k \rightarrow v_\pi=\left(I-\gamma P_\pi\right)^{-1} r_\pi, \quad k \rightarrow \infty \]
Proof: the closed-form solution
First, the Bellman equation in matrix-vector form is \[ v_\pi=r_\pi+\gamma P_\pi v_\pi . \] Put the \(\gamma P_\pi v_\pi\) into the left side: \[ \begin{aligned} v_\pi - \gamma P_\pi v_\pi =r_\pi \\ (I - \gamma P_\pi) v_\pi = r_\pi \end{aligned} \]
Now we calculate the matrix inverse: \[ v_\pi=\left(I-\gamma P_\pi\right)^{-1} r_\pi . \] Q.E.D.
Proof: the iterative solution
Define the error as \(\delta_k=v_k-v_\pi\). We only need to show \(\delta_k \rightarrow 0\). Substituting:
- \(v_{k+1}=\delta_{k+1}+v_\pi\) and
- \(v_k=\delta_k+v_\pi\)
into \(v_{k+1}=r_\pi+\gamma P_\pi v_k\) gives \[ \delta_{k+1}+v_\pi=r_\pi+\gamma P_\pi\left(\delta_k+v_\pi\right) \] which can be rewritten as \[ \delta_{k+1}=-v_\pi+r_\pi+\gamma P_\pi \delta_k+\gamma P_\pi v_\pi=\gamma P_\pi \delta_k \]
As a result, \[ \delta_{k+1}=\gamma P_\pi \delta_k=\gamma^2 P_\pi^2 \delta_{k-1}=\cdots=\gamma^{k+1} P_\pi^{k+1} \delta_0 \]
Note that \(0 \leq P_\pi^k \leq 1\), which means every entry of \(P_\pi^k\) is no greater than 1 for any \(k=0,1,2, \ldots\). That is because \(P_\pi^k \mathbf{1}=\mathbf{1}\), where \(\mathbf{1}=[1, \ldots, 1]^T\). On the other hand, since \(\gamma<1\), we know \(\gamma^k \rightarrow 0\) and hence \[ \delta_{k+1}=\gamma^{k+1} P_\pi^{k+1} \delta_0 = \gamma P_k^{\pi}(\gamma^{k} P_\pi^{k} \delta_0) \rightarrow 0 \] as \(k \rightarrow \infty\).