Asymptotic Equipartition Property
Sources:
- EE 376A: Information Theory. Winter 2018. Lecture 4. - Stanford University
- EE 376A: Information Theory. Winter 2017. Lecture 4. - Stanford University
- Elements of Information Theory
Intro
In information theory, the analog of the law of large numbers(LLN) is the asymptotic equipartition property (AEP).
It is a direct consequence of the weak law of large numbers.
The law of large numbers states that for iid random variables,
The AEP states that
This enables us to divide the set of all sequences into two sets, the typical set, where the sample entropy is close to the true entropy, and the nontypical set, which contains the other sequences.
Most of our attention will be on the typical sequences. Any property that is proved for the typical sequences will then be true with high probability and will determine the average behavior of a large sample.
Notation
Memoryless source:
- Note: All i.i.d. r.v. have the same probability distribution and the same entropy.
Alphabet:
Source sequence:
- Since the source symbols are memoryless here.
- Since the source symbols are memoryless here.
Probability of
The
Definition: For some
Let
即:
Furthermore, note the following equivalent ways of defining
We have
From
Theorem:
Theorem:
Proof
Note that
Also, we know that
Note that since
Recalling that by the definition of entrypy,
Note: Since
AEP
From Theorem:
From
As a result,
for
Thus, AEP enables us to partition the sequence
- Typical set: Containing sequences with probability close to
- Atypical set: Containing the other sequences.
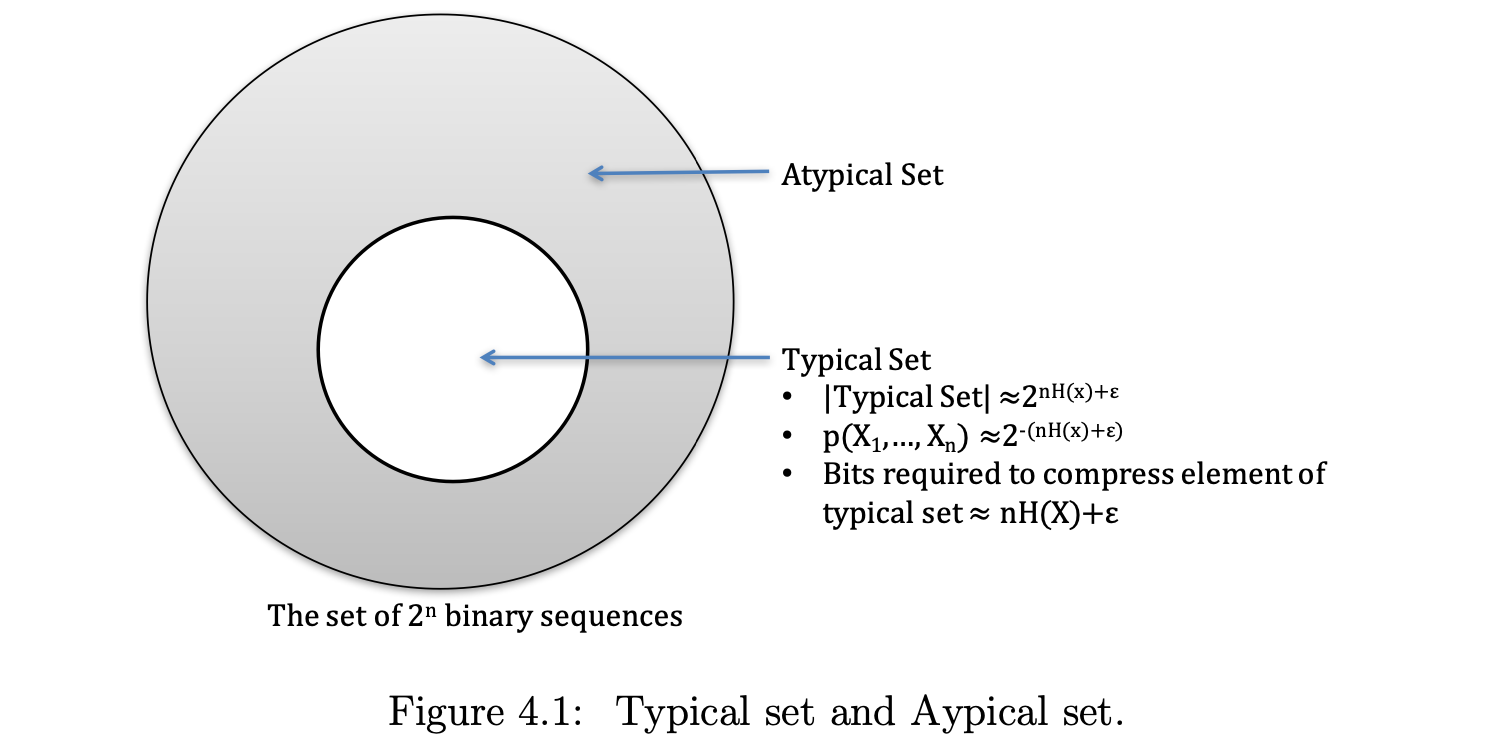
Note: the notation
Theorem: Bound of
Theorem:
Proof
Upper bound:
See following equation:
According to
Lower bound:
See following equation:
The starting equation
Since
According to
Theorem:
The space of all possible source sequences
In fact,
Despite the small size of
Theorem:
Theorem: Fix
Proof
$$
Explaination:
Then, we have
Then
The limit in
From the theorems proven above, we understand
Appendix
Proof of
Inclusion (
Let
- If
- If
Therefore,
- If
Inclusion (
Let
- If
- If
Since
Therefore,
Combining both inclusions, we have
- If