Relations and Digraphs

Posted on 2023-08-15 Edited on 2025-11-25 In Mathematics Views: 113

Sources:

Bernard Kolman, Robert C. Busby & Sharon Cutler Ros. (2014). Relations and Digraph. Discrete Mathematical Structures (6th ed., pp. 139-204). Pearson.

Orderd pair and list

List:
- Suppose 𝑛 is a nonnegative integer. A list of length 𝑛 is an ordered collection of 𝑛 elements (which might be numbers, other lists, or more abstract objects).
  - Note: A list has finite length since $n$ is an integer.
- Two lists are equal if and only if they have the same length and the same elements in the same order.
Ordered pair:
- An ordered pair $(a, b)$ is a listing of the objects a and b in a prescribed order, with a appearing first and b appearing second.
- Thus an ordered pair is merely a sequence of length 2.

Product Sets

If A and B are two nonempty sets, we define the product set or Cartesian product $A \times B$ as the set of all ordered pairs (a,b) with a∈A and b∈B. Thus $A \times B = {(a, b) | a \in A and b \in B}$

Theorem:

For any two finite, nonempty sets $A$ and $B$ , $| A \times B | = | A | | B |$ .

Proof:

Suppose that |A| = m and |B| = n. To form an ordered pair (a,b), a ∈ A and b ∈ B, 需要分别从A, B中选一个元素, 分别有m, n中可能, 因此 $| A \times B | = m \cdot n = | A | \cdot | B |$ .

Example:

If $A = B = R$ , the set of all real numbers, then $R \times R$ , also denoted by $R^{2}$ , is the set of all points in the plane. The ordered pair $(a, b)$ gives the coordinates of a point in the plane.

Partitions

A partition(划分) or quotient set(商集) of a nonempty set $A$ is a set $P$ of nonempty subsets of A such that:

Each element of $A$ belongs to one of the sets in $P$ .
If $A_{1}$ and $A_{2}$ are distinct elements of $P$ , then $A_{1} \cap A_{2} = \emptyset$ .

即: 集合 $A$ 的划分 $P$ 是 $A$ 的子集的集合.

The sets in $P$ are called the blocks or cells of the partition. Below figure shows a partition $P = A_{1}, A_{2}, A_{3}, A_{4}, A_{5}, A_{6}, A_{7}$ of $A$ into seven blocks:

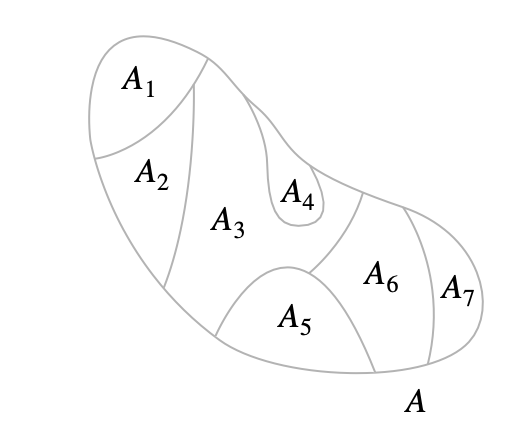
Since the members of a partition of a set $A$ are subsets of $A$ , we see that the partition is a subset of $P (A)$ , the power set of $A$ . That is, partitions can be considered as particular kinds of subsets of $P (A)$ . 集合A的划分是A的幂集的一个子集.

Example:

Let $A = a, b, c, d, e, f, g, h$ . Consider the following subsets of $A$ : $\begin{aligned} A_{1} & = a, b, c, d \\ A_{2} & = a, c, e, f, g, h \\ A_{3} & = a, c, e, g \\ A_{4} & = b, d \\ A_{5} & = f, h \end{aligned}$

Then $A_{1}, A_{2}$ is not a partition since $A_{1} \land A_{2} \neq \emptyset$ .

Also, ${A_{1}, A 5}$ is not a partition since $e \notin A_{1}$ and $e \notin A_{5}$ .

The collection $P = A_{3}, A_{4}, A_{5}$ is a partition of $A$ .

Example:

Let

$\begin{aligned} Z & = set of all integers, \\ A_{1} & = set of all even integers, and \\ A_{2} & = set of all odd integers. \end{aligned}$

Then ${A_{1}, A_{2}}$ is a partition of $Z$ .

Relations

Let $A$ and $B$ be nonempty sets. A relation $R$ from $A$ to $B$ is a subset of $A \times B$ .

If $R \subseteq A \times B$ and $(a, b) \in R$ , we say that $a$ is related to $b$ by $R$ , and we also write $a R b$ .

If $a$ is not related to $b$ by R, we write $a R̸ b$ .

Frequently, $A$ and $B$ are equal. In this case, we often say that $R \subseteq A \times A$ is a relation on $A$ , instead of a relation from $A$ to $A$ .

Example:

Let $A = 1, 2, 3$ and $B = r, s$ . Then $R = {(1, r), (2, s), (3, r)}$ is a relation from $A$ to $B$ .

Example:

实数域的"等于"

Let $A$ and $B$ be sets of real numbers. We define the following relation $R$ (equals) from $A$ to $B$ : $a R b if and only if a = b .$

Example:

实数域的"小于"

Let $A = 1, 2, 3, 4, 5$ . Define the following relation $R$ (less than) on $A$ : $a R b if and only if a < b .$ Then

R = {(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5)}.

Sets Arising from Relations

Domain and Range

The domain of $R$ , denoted by $Dom (R)$ , is the set of elements in $A$ that are related to some element in $B$ .

In other words, $Dom (R)$ , a subset of $A$ , is the set of all first elements in the pairs that make up $R$ .
The range, or codomain of $R$ , denoted by $Ran (R)$ , is the set of elements in $B$ that are second elements of pairs in $R$ , that is, all elements in $B$ that are paired with some element in $A$ .
Elements of $A$ that are not in $Dom (R)$ are not involved in the relation $R$ in any way. This is also true for elements of $B$ that are not in $Ran (R)$ .

R-relative Set

$R$ -relative set(R相关集): If $R$ is a relation from A to B and $x \in A$ , we define $R (x)$ , the $R$ -relative set of $x$ , to be the set of all $y$ in $B$ with the property that $x$ is $R$ -related to $y$ . Thus, in symbols, $R (x) = {y \in B | x R y} .$
Similarly, if $A_{1} \subseteq A$ , then $R (A_{1})$ , the $R$ -relative set of $A_{1}$ , is the set of all $y$ in $B$ with the property that $x$ is $R$ -related to $y$ for some $x$ in $A_{1}$ . That is, $R (A_{1}) = {y \in B | x R y for some x \ in A_{1}}$
Note that $R (x)$ can also be written as $R ({x})$ , but we choose the simpler notation.
我们定义 $R (A_{1})$ is the union of the sets $R (x)$ , where $x \in A_{1}$ .
- 当参数为元素 $x$ 时, $R (x)$ 表示 $x$ 的 $R$ 相关集. 当参数为集合 $A$ 时, $R (A)$ 表示 $A$ 中每一个元素 $x$ 的 $R$ 相关集的union(并集).

THEOREM1

Let $R$ be a relation from $A$ to $B$ , and let $A_{1}$ and $A_{2}$ be subsets of $A$ . Then:

If $A_{1} \subseteq A_{2}$ , then $R (A_{1}) \subseteq R (A_{2})$ .
$R (A_{1} \cup A_{2}) = R (A_{1}) \cup R (A_{2})$ .
$R (A_{1} \cap A_{2}) \subseteq R (A_{1}) \cap R (A_{2})$ .

Proof

If $y \in R (A_{1})$ ,then $x R y$ for some $x \in A_{1}$ . Since $A_{1} \subseteq A_{2}$ , $x \in A_{2}$ . 因此在 $A_{2}$ 中存在若干个 $x$ 满足 $x R y$ , 即存在 $(x, y), x \in A_{2}$ . Thus, $y \in R (A_{2})$ , 因此证明了(1).
If $y \in R (A_{1} \cup A_{2})$ ,then by definition $x R y$ for some $x$ in $A_{1} \cup A_{2}$ . If $x$ is in $A_{1}$ , then, since $x R y$ , we must have $y \in R (A_{1})$ .

By the same argument, if $x$ is in $A_{2}$ , then $y \in R (A_{2})$ . In either case, $y \in R (A_{1}) \cup R (A_{2})$ . Thus we have shown that $R (A_{1} \cup A_{2}) \subseteq R (A_{1}) \cup R (A_{2})$ .

Conversely, since $A_{1} \subseteq (A_{1} \cup A_{2})$ , part (1) tells us that $R (A_{1}) \subseteq R (A_{1} \cup A_{2})$ . Similarly, $R (A_{2}) \subseteq R (A_{1} \cup A_{2})$ . Thus R(A_1) ∪ $R (A_{2}) \subseteq R (A_{1} \cup A_{2})$ , and therefore part (2) is true.
If $y \in R (A_{1} \cap A_{2})$ , then, for some $x$ in $A_{1} \cap A_{2}$ , $x R y$ . Since $x$ is in both $A_{1}$ and $A_{2}$ , it follows that y is in both $R (A_{1})$ and $R (A_{2})$ ; that is, $y \in R (A_{1}) \cap R (A_{2})$ . Thus part (3) holds.

THEOREM2

Let $R$ and $S$ be relations from $A$ to. $B$ . If $R (a) = S (a)$ for all $a$ in $A$ , then $R = S$ .

Proof

If $a R b$ , then $b \in R (a)$ . Therefore, $b \in S (a)$ and $a S b$ . A completely similar argument shows that, if $a S b$ , then $a R b$ .

由于每个 $a R b$ 都有 $a S b$ , 所以 $R \subset S$ ; 反之得到 $S \subset A$ , 因此有 $R = S$ .

The Matrix of a Relation

We can represent a relation between two finite sets with a matrix as follows. If $A = a_{1}, a_{2}, . . ., a m$ and $B = b 1, b 2, . . ., b n$ are finite sets containing $m$ and $n$ elements, respectively, and $R$ is a relation from $A$ to $B$ , we represent $R$ by the $m \times n$ matrix $M_{R} = [m_{i j}]$ , which is defined by $m_{i j} = {\begin{cases} 1 & if (a_{i}, b_{j}) \in R \\ 0 & if (a_{i}, b_{j}) \notin R . \end{cases}$

The matrix $M_{R}$ is called the matrix of $R$ . Often $M_{R}$ provides an easy way to check whether $R$ has a given property.

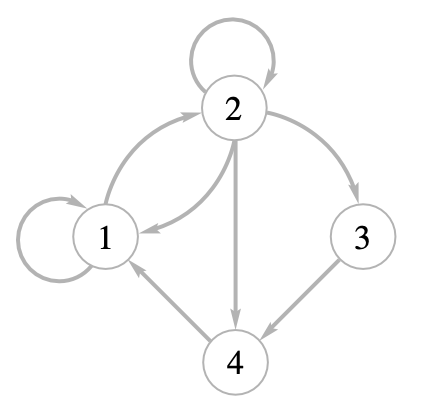
The Digraph of a Relation

Digraphs are nothing but geometrical representations of relations.

If $A$ is a finite set(有限集合) and $R$ is a relation on $A$ , we can also represent $R$ pictorially as follows:

$A$ 中的每个元素都是一个点(vertex)
点 $a_{i}$ 和 $a_{j}$ 存在一条边(edge) iff $a_{i} R a_{j}$ .

The resulting pictorial representation of $R$ is called a directed graph or digraph of $R$ .

可以看到, $R$ 是 $A$ 上的关系. 也就是说digrapg中的R是从A映射到A的, 这也说明了图上的点只能连接到图上的其他点, 不能连接到别的奇奇怪怪的地方.

Example:

Let $\begin{aligned} A & = {1, 2, 3, 4} \\ R & = {(1, 1), (1, 2), (2, 1), (2, 2), (2, 3), (2, 4), (3, 4), (4, 1)} . \end{aligned}$

Then the digraph of $R$ is as shown in below:

In-degree & Out-degree

If R is a relation on a set A and a ∈ A, then

The in-degree(入度) of $a$ (relative to the relation $R$ ) is the number of $b \in A$ such that $(b, a) \in R$ .
The out-degree(出度) of $a$ is the number of $b \in A$ such that $(a, b) \in R$ .

在图像上, 一个vertex的in-degree代表指向该vertex的edge, 而out-degree代表从该vertex出发的edge.

Note that the out-degree of $a$ is $| R (a) |$ .

Paths in Relations and Digraphs

A path is most easily visualized with the aid of the digraph of the relation. It appears as a geometric path or succession of edges in such a digraph.

Suppose that $R$ is a relation on a set $A$ .

A path of length $n$ in $R$ from $a$ to $b$ is a finite sequence $π : a, x_{1}, x_{2}, . . ., x_{n - 1}, b$ , beginning with $a$ and ending with $b$ , such that $a R x_{1}, x_{1} R x_{2}, \dots, x_{n - 1} R b .$

Note that a path of length $n$ involves $n + 1$ elements of $A$ , although they are not necessarily distinct.

cycle(环): A path that begins and ends at the same vertex is called a cycle(环).
It is clear that the paths of length $1$ can be identified with the ordered pairs $(x, y)$ that belong to $R$ .
$R^{n}$ : If $n$ is a fixed positive integer, we define a relation $R^{n}$ on $A$ as follows: $x R^{n} y$ means that there is a path of length $n$ from $x$ to $y$ in $R$ . 即存在一条x -> y的长度为n的路径.
- $R^{n} (x)$ consists of all vertices that can be reached from $x$ by means of a path in $R$ of length $n$ .
$R^{\infty}$ : The connectivity(连通性) relation $R^{\infty}$ of a relation $R$ on a set $A$ mean that if by letting $x R^{\infty} y$ , there is some path in $R$ from $x$ to $y$ . $R^{\infty}$ 也被称为connectivity(连通性). 即存在一条x -> y的长度未知的路径.
- The set $R^{\infty} (x)$ consists of all vertices that can be reached from $x$ by some path in $R$ .
$R^{*}$ : The reachability(可达性) relation $R^{*}$ of a relation $R$ on a set $A$ that has $n$ elements is defined asfollows:

$x R^{*} y$ means that $x = y$ or $x R^{\infty} y$ . The idea is that $y$ is reachable from $x$ if either $y$ is $x$ or there is some path from $x$ to $y$ . y到x是可达的 = 要么y就是x, 要么存在一条x -> y的长度未知的路径.
- It is easily seen that $M_{R^{*}} = M_{R^{\infty}} \lor I_{n}$ , where $I_{n}$ is the $n \times n$ identity matrix.
路径的组合:

Let $π_{1} : a, x_{1}, x_{2}, \dots, x_{n - 1}, b$ be a path in a relation $R$ of length $n$ from $a$ to $b$ , and let $π_{2} : b, y_{1}, y_{2}, . . ., y_{m - 1}, c$ be a path in $R$ of length $m$ from $b$ to $c$ .

Then the composition of $π_{1}$ and π2 $π_{2}$ the path $a, x_{1}, x_{2}, . . ., b, y_{1}, y_{2}, . . ., y_{m - 1}, c$ of length $n + m$ , which is denoted by $π_{2} ◦ π_{1}$ . This is a path from $a$ to $c$ .

即: 如果有一条长度为m的路径 $π_{1}$ : a -> ... -> b, 长度为n的路径 $π_{2}$ : b -> ... -> c. 则存在从a到c的路径a -> ... -> b -> ... -> c, 它是 $π_{1}$ 和 $π_{2}$ 的组合, 长度为m+n.

Theorem:

If $R$ is a relation on $A = {a_{1}, a_{2}, . . ., a n}$ , then $M_{R^{2}} = M_{R} ⊙ M_{R}$

Proof:
Let $M_{R} = m_{i j}$ and $M_{R^{2}} = n_{i j}$ . By definition, the $i, j$ th element of is $M_{R} ⊙ M_{R}$ equal to $1$ if and only if row $i$ of $M_{R}$ and column $j$ of $M_{R}$ have a $1$ in the same relative position, say position $k$ . This means that $m_{i k} = 1$ and $m_{k j} = 1$ for some $k, 1 \leq k \leq n$ .

By definition of the matrix $M_{R}$ , the preceding conditions mean that $a_{i} R a_{k}$ and $a_{k} R a_{j}$ . Thus $a_{i} R^{2} a_{j}$ , and so $n_{i j} = 1$ . We have therefore shown that position $i, j$ of $M_{R} ⊙ M_{R}$ is equal to $1$ if and only if $n_{i j} = 1$ . This means that $M_{R} ⊙ M_{R} = M_{R^{2}}$ .

翻译:

如果 $M_{R} ⊙ M_{R}$ 的i,j元素为1, 当且仅当 $M_{R}$ 的第i行和 $M_{R}$ 的第k列的对应位置(记为k)存在一个1, 即 $m_{i k} = 1$ and $m_{k j} = 1$ for some $k, 1 \leq k \leq n$ . 根据 $M_{R}$ 的定义, 这意味着 $a_{i} R a_{k}$ and $a_{k} R a_{j}$ , 因此存在长度为2的路径i->k->j, 因此有 $a_{i} R^{2} a_{j}$ , 所以有 $n_{i j} = 1$ .

这意味着: $M_{R} ⊙ M_{R}$ 的i,j元素为1 iff $n_{i j} = 1$ . 也就是 $M_{R} ⊙ M_{R} = M_{R^{2}}$ .

For brevity, we will usually denote $M_{R} ⊙ M_{R}$ . simply as $(M_{R})_{⊙}^{2}$ (the symbol $⊙$ reminds us that this is not the usual matrix product).

Theorem:

之前的结论可以推导到n>=2:

For $n \geq 2$ and $R$ a relation on a finite set $A$ , we have $M_{R^{n}} = M_{R} ⊙ M_{R} ⊙ \dots ⊙ M_{R} (n factors) .$ 证明略.

联系之前 $R^{*}$ 的定义, 可得: $M_{R^{*}} = I_{n} \lor M_{R} \lor (M_{R})_{⊙}^{2} \lor (M_{R})_{⊙}^{3} \lor \dots .$

Equivalence Relations

equivalence relation(等价关系): A relation R on a set A is called an equivalence relation if it is reflexive, symmetric, and transitive. 即同时满足自反性, 对称性和传递性.

Example:

Let $A$ be the set of all triangles in the plane and let $R$ be the relation on $A$ defined as follows: $R = {(a, b) \in A \times A ∣ a is congruent to b} .$ It is easy to see that $R$ is an equivalence relation.

Example:

Let $A = {1, 2, 3, 4}$ and let $R = {(1, 1), (1, 2), (2, 1), (2, 2), (3, 4), (4, 3), (3, 3), (4, 4)}$ It is easy to verify that $R$ is an equivalence relation.

Equivalence Relations and Partitions

THEOREM 1: Equivalence Relation -> Partition

如果 $P$ 是集合 $A$ 上的一个划分(partition), 那么可以用 $P$ 来构建一个等价关系.

Let $P$ be a partition of a set $A$ . Recall that the sets in $P$ are called the blocks of $P$ . Define the relation $R$ on $A$ as follows: $a R b if and only if a and b are members of the same block .$

Then $R$ is an equivalence relation on $A$ .

Proof:

If $a \in A$ , then clearly $a$ is in the same block as itself; so $a R a$ . 自反性.
If $a R b$ , then $a$ and $b$ are in the same block; so $b R a$ . 如果 $a R b$ , 则a, b在同一个block内, 因此必定有 $b R a$ , 证明了对称性.
If $a R b$ and $b R c$ , then $a, b$ , and $c$ must all lie in the same block of $P$ . Thus $a R c$ . 如果 $a R b$ , 则a, b在同一个block内, 同理b, c也在同一个block内, 因此a, b, c都在同一个block内, 因此有 $a R c$ . 证明了传递性.

因此 $R$ 是自反, 对称且传递的.

$R$ will be called the equivalence relation determined by $P$ .

Since $R$ is reflexive, symmetric, and transitive, $R$ is an equivalence relation.

THEOREM 2: Partition -> Equivalence Relation

反过来, 也可以用等价关系 $R$ 来构建划分 $P$ .

Let $R$ be an equivalence relation on $A$ , and let $P$ be the collection of all distinct relative sets $R (a)$ for $a$ in $A$ .

Then $P$ is a partition of $A$ , and $R$ is the equivalence relation determined by $P$ .

Proof: According to the definition of a partition, we must show the following two properties:

Every element of $A$ belongs to some relative set(some $R (a)$ ).
If $R (a)$ and $R (b)$ are not identical, then $R (a) \cap R (b) = \emptyset$ .

由于 $R$ 具有自反性, 我们有 $a \in R (a)$ , 因此证明了性质1.

接着证明性质2的逆否命题: $If R (a) \cap R (b) \neq \emptyset, then R (a) = R (b) .$

To prove this, we assume that $c \in R (a) \cap R (b)$ . Then $a R c$ and $b R c$ .

Since $R$ is symmetric, we have $c R b$ .

Then $a R c$ and $c R b$ , so, by transitivity of $R$ , $a R b$ .

Lemma1已经证明了 $a R b ⟺ R (a) = R (b)$ . 证明结束.

We have now proved that $P$ is a partition. By Lemma 1 we see that $a R b$ if and only if $a$ and $b$ belong to the same block of $P$ . Thus $P$ determines $R$ , and the theorem is proved. Note the use of the contrapositive in this proof. If $R$ is an equivalence relation on $A$ , then the sets $R (a)$ are traditionally called equivalence classes of $R$ . Some authors denote the class $R (a)$ by $[a]$ . The partition $P$ constructed in Theorem 2 therefore consists of all equivalence classes of $R$ , and this partition will be denoted by $A / R$ . Recall that partitions of $A$ are also called quotient sets of $A$ , and the notation $A / R$ reminds us that $P$ is the quotient set of $A$ that is constructed from and determines $R$ .

Lemma1

Let $R$ be an equivalence relation on a set $A$ , and let $a \in A$ and $b \in A$ . Then $a R b ⟺ R (a) = R (b)$

Proof

充分性: 假设 $R (a) = R (b)$ , 由于 $R$ 是自反的, 因此有 $b \in R (b)$ , 因此有 $b \in$ $R (a)$ , 因此有 $a R b$ .

必要性:

假设 $a R b$ . Then note that

由于 $R$ 是对称的, 所以有 $b R a$ .
$\forall x \in R (b)$ , 有 $b R x$ . 由于 $R$ 是传递的, 并且已经有 $a R b$ , 所以有 $a R c$ , 也就是说: $\forall x \in R (b), x \in R (a)$ . 证明了 $R (b) \subseteq R (a)$ .
反过来, $\forall y \in R (a)$ , 有 $a R y$ . 由于 $R$ 是传递的, 并且已经有 $b R a$ , 所以有 $b R y$ , 也就是说: $\forall y \in R (a), x \in R (a)$ . 证明了 $R (a) \subseteq R (b)$ .
综上所述, $R (a) = R (b)$ .

Equivalence Class

equivalence class(等价类): If $R$ is an equivalence relation on $A$ , then the sets $R (a)$ are traditionally called equivalence classes of $R$ .

这里的 $R (a)$ 指的是THEOREM2中的distinct relative set $R (a)$ for $a$ in $A$ . 每个不同(distinct)的 $R (a)$ 就是一个等价类.
划分 $P$ 就是 $R$ 的等价类构成的集合. $P$ 被表示为 $A / R$ .
由于 $P$ 也被称为A的商集(quotient set), the notation $A / R$ reminds us that $P$ is the quotient set of $A$ that is constructed from and determines $R$ .
Some authors denote the equivalence class $R (a)$ by $[a]$ .

Transitive Closure and Warshall's Algorithm

Transitive Closure

In this section we consider a construction that has several interpretations and many important applications. Suppose that R is a relation on a set A and that R is not transitive. We will show that the transitive closure of R (see Section 7) is just the connectivity relation $R^{\infty}$ , defined in Section 3.