Relations and Digraphs

Posted on 2023-08-15 Edited on 2024-09-17 In Mathematics Views:

Sources:

Bernard Kolman, Robert C. Busby & Sharon Cutler Ros. (2014). Relations and Digraph. Discrete Mathematical Structures (6th ed., pp. 139-204). Pearson.

Product Sets

An ordered pair $(a, b)$ is a listing of the objects a and b in a prescribed order, with a appearing first and b appearing second. Thus an ordered pair is merely a sequence of length 2. It follows that the ordered pairs $(a_1 , b1 )$ and $(a_2 , b2 )$ are equal if and only if $a_1 =a2$ and $b1 =b2$.

If A and B are two nonempty sets, we define the product set or Cartesian product $A\times B$ as the set of all ordered pairs (a,b) with a∈A and b∈B. Thus \[ A \times B = \{(a, b) | a ∈ A \ \ \text{and} \ \ b ∈ B\} \]

Theorem:

For any two finite, nonempty sets $A$ and $B$, $|A × B| = |A| |B|$.

Proof:

Suppose that |A| = m and |B| = n. To form an ordered pair (a,b), a ∈ A and b ∈ B, 需要分别从A, B中选一个元素, 分别有m, n中可能, 因此$|A × B| = m · n = |A| · |B|$.

Example:

If $A=B=\mathbb{R}$, the set of all real numbers, then $\mathbb{R} \times \mathbb{R}$, also denoted by $\mathbb{R} ^ 2$, is the set of all points in the plane. The ordered pair $(a, b)$ gives the coordinates of a point in the plane.

Partitions

A partition(划分) or quotient set(商集) of a nonempty set $A$ is a set $\mathcal{P}$ of nonempty subsets of A such that:

Each element of $A$ belongs to one of the sets in $\mathcal{P}$.
If $A_1$ and $A_2 $ are distinct elements of $\mathcal{P}$, then $A_1 \cap A_2 = \emptyset$.

即: 集合$A$的划分 $\mathcal{P}$ 是$A$的子集的集合.

The sets in $\mathcal{P}$ are called the blocks or cells of the partition. Below figure shows a partition $\mathcal{P}={A_1,A_2,A_3,A_4,A_5,A_6,A_7}$ of $A$ into seven blocks:

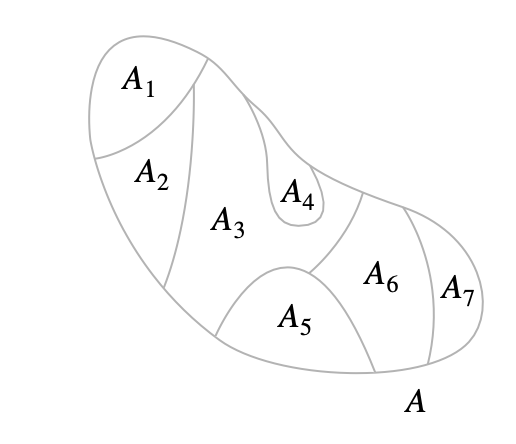
Since the members of a partition of a set $A$ are subsets of $A$, we see that the partition is a subset of $P(A)$, the power set of $A$. That is, partitions can be considered as particular kinds of subsets of $P(A)$. 集合A的划分是A的幂集的一个子集.

Example:

Let $A = {a, b, c, d, e, f, g, h}$. Consider the following subsets of $A$: \[ \begin{align} A_1 &= {a,b,c,d} \nonumber \\ A_2 &= {a,c,e,f,g,h} \nonumber \\ A_3 &= {a,c,e,g}\nonumber \\ A_4 &={b,d}\nonumber \\ A_5 &={f,h} \nonumber \end{align} \]

Then ${A_1, A_2}$ is not a partition since $A_1 \wedge A_2 \ne \emptyset$.

Also, $\{A_1, A5\}$ is not a partition since $e \notin A_1$ and $e \notin A_5$.

The collection $\mathcal{P} = {A_3,A_4,A_5}$ is a partition of $A$.

Example:

Let

\[ \begin{align} \mathbb{Z} &= \text{set of all integers,} \nonumber \\ A_1 &= \text{set of all even integers, and} \nonumber \\ A_2 &= \text{set of all odd integers.} \nonumber \end{align} \]

Then $\{A_1, A_2\}$ is a partition of $\mathbb{Z}$.

Relations

Let $A$ and $B$ be nonempty sets. A relation $R$ from $A$ to $B$ is a subset of $A×B$.

If $R ⊆ A × B$ and $(a, b) ∈ R$, we say that $a$ is related to $b$ by $R$, and we also write $a \ R \ b$.

If $a$ is not related to $b$ by R, we write $a \ \not R \ b$.

Frequently, $A$ and $B$ are equal. In this case, we often say that $R ⊆ A × A$ is a relation on $A$, instead of a relation from $A$ to $A$.

Example:

Let $A = {1,2,3}$ and $B = {r,s}$. Then $R = \{ (1,r),(2,s),(3,r) \}$ is a relation from $A$ to $B$.

Example:

实数域的"等于"

Let $A$ and $B$ be sets of real numbers. We define the following relation $R$ (equals) from $A$ to $B$: \[ a \ R \ b \ \text{ if and only if} \ a=b. \]

Example:

实数域的"小于"

Let $A = {1, 2, 3, 4, 5}$. Define the following relation $R$ (less than) on $A$: \[ a \ R \ b \ \text{ if and only if} \ a<b. \] Then

R = {(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5)}.

Sets Arising from Relations

Domain and Range

The domain of $R$, denoted by $\text{Dom}(R)$, is the set of elements in $A$ that are related to some element in $B$.

In other words, $\text{Dom}(R)$, a subset of $A$, is the set of all first elements in the pairs that make up $R$.
The range, or codomain of $R$, denoted by $\text{Ran}(R)$, is the set of elements in $B$ that are second elements of pairs in $R$, that is, all elements in $B$ that are paired with some element in $A$.
Elements of $A$ that are not in $\text{Dom}(R)$ are not involved in the relation $R$ in any way. This is also true for elements of $B$ that are not in $\text{Ran}(R)$.

R-relative Set

$R$-relative set(R相关集): If $R$ is a relation from A to B and $x ∈ A$, we define $R(x)$, the $R$-relative set of $x$, to be the set of all $y$ in $B$ with the property that $x$ is $R$-related to $y$. Thus, in symbols, \[ R(x) = \{y ∈ B | \ x \ R \ y\}. \]
Similarly, if $A_1 ⊆ A$, then $R(A_1)$, the $R$-relative set of $A_1$, is the set of all $y$ in $B$ with the property that $x$ is $R$-related to $y$ for some $x$ in $A_1$. That is, \[ R(A_1) = \{ y ∈ B \ | \ x \ R \ y \ \text{for some x \ in} \ A_1 \} \]
Note that $R(x)$ can also be written as $R(\{x\})$, but we choose the simpler notation.
我们定义 $R(A_1)$ is the union of the sets $R(x)$, where $x ∈ A_1$.
- 当参数为元素$x$时, $R(x)$表示$x$的$R$相关集. 当参数为集合$A$时, $R(A)$表示$A$中每一个元素$x$的$R$相关集的union(并集).

THEOREM1

Let $R$ be a relation from $A$ to $B$, and let $A_1$ and $A_2$ be subsets of $A$. Then:

If $A_1 ⊆ A_2$, then $R(A_1) ⊆ R(A_2)$.
$R(A_1 ∪ A_2) = R(A_1) ∪ R(A_2)$.
$R(A_1∩A_2)⊆R(A_1)∩R(A_2)$.

Proof

If $y ∈ R(A_1)$,then $x \ R \ y$ for some $x∈A_1$. Since $A_1 ⊆A_2$, $x∈A_2$. 因此在$A_2$中存在若干个$x$满足 $x \ R \ y$, 即存在$( x, y ), \ x \in A_2$. Thus, $y ∈ R(A_2)$, 因此证明了(1).
If $y∈R(A_1 ∪ A_2)$,then by definition $x \ R \ y$ for some $x$ in $A_1∪A_2$. If $x$ is in $A_1$, then, since $x \ R \ y$, we must have $y ∈ R(A_1)$.

By the same argument, if $x$ is in $A_2$, then $y ∈ R(A_2)$. In either case, $y ∈ R(A_1) ∪ R(A_2)$. Thus we have shown that $R(A_1 ∪ A_2) ⊆ R(A_1) ∪ R(A_2)$.

Conversely, since $A_1 ⊆ (A_1 ∪ A_2)$, part (1) tells us that $R(A_1) ⊆ R(A_1 ∪ A_2)$. Similarly, $R(A_2) ⊆ R(A_1 ∪ A_2)$. Thus R(A_1) ∪ $R(A_2) ⊆ R(A_1 ∪ A_2)$, and therefore part (2) is true.
If $y∈R(A_1∩A_2)$, then, for some $x$ in $A_1∩A_2$, $x \ R \ y$. Since $x$ is in both $A_1$ and $A_2$, it follows that y is in both $R(A_1)$ and $R(A_2)$; that is, $y ∈ R(A_1) ∩ R(A_2)$. Thus part (3) holds.

THEOREM2

Let $R$ and $S$ be relations from $A$ to. $B$. If $R(a)=S(a)$ for all $a$ in $A$, then $R=S$.

Proof

If $a \ R \ b$, then $b ∈ R(a)$. Therefore, $b ∈ S(a)$ and $a \ S \ b$. A completely similar argument shows that, if $a \ S \ b$, then $a \ R \ b$.

由于每个$a \ R \ b$都有$a \ S \ b$, 所以$R \subset S$; 反之得到$S \subset A$, 因此有$R = S$.

The Matrix of a Relation

We can represent a relation between two finite sets with a matrix as follows. If $A = {a_1,a_2,...,am}$ and $B = {b1,b2,...,bn}$ are finite sets containing $m$ and $n$ elements, respectively, and $R$ is a relation from $A$ to $B$, we represent $R$ by the $m×n$ matrix $M_R = [m_{ij}]$ , which is defined by \[ m_{i j}=\left\{\begin{array}{ll} 1 & \text { if }\left(a_{i}, b_{j}\right) \in R \\ 0 & \text { if }\left(a_{i}, b_{j}\right) \notin R . \end{array}\right. \]

The matrix $M_R$ is called the matrix of $R$. Often $M_R$ provides an easy way to check whether $R$ has a given property.

The Digraph of a Relation

Digraphs are nothing but geometrical representations of relations.

If $A$ is a finite set(有限集合) and $R$ is a relation on $A$, we can also represent $R$ pictorially as follows:

$A$中的每个元素都是一个点(vertex)
点 $a_i$和 $a_j$存在一条边(edge) iff $a_i \ R \ a_j$.

The resulting pictorial representation of $R$ is called a directed graph or digraph of $R$.

可以看到, $R$是$A$上的关系. 也就是说digrapg中的R是从A映射到A的, 这也说明了图上的点只能连接到图上的其他点, 不能连接到别的奇奇怪怪的地方.

Example:

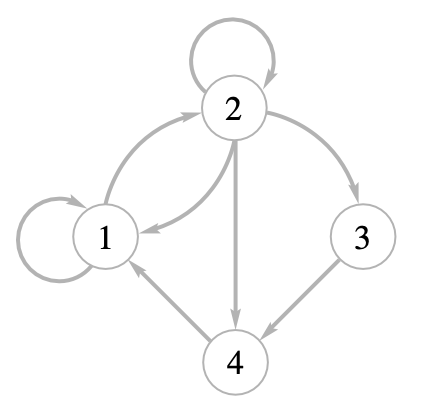
Let \[ \begin{align} A &= \{1,2,3,4\} \nonumber \\ R &= \{(1, 1), (1, 2), (2, 1), (2, 2), (2, 3), (2, 4), (3, 4), (4, 1)\}. \nonumber \end{align} \]

Then the digraph of $R$ is as shown in below:

In-degree & Out-degree

If R is a relation on a set A and a ∈ A, then

The in-degree(入度) of $a$ (relative to the relation $R$) is the number of $b ∈ A$ such that $(b, a) \in R$.
The out-degree(出度) of $a$ is the number of $b ∈ A$ such that $(a, b) ∈ R$.

在图像上, 一个vertex的in-degree代表指向该vertex的edge, 而out-degree代表从该vertex出发的edge.

Note that the out-degree of $a$ is $|R(a)|$.

Paths in Relations and Digraphs

A path is most easily visualized with the aid of the digraph of the relation. It appears as a geometric path or succession of edges in such a digraph.

Suppose that $R$ is a relation on a set $A$.

A path of length $n$ in $R$ from $a$ to $b$ is a finite sequence $π : a, x_1, x_2, . . . , x_{n−1}, b$, beginning with $a$ and ending with $b$, such that \[ a \ R \ x_1, \ x_1 \ R \ x_2, \ \dots, \ x_{n−1} \ R \ b. \]

Note that a path of length $n$ involves $n + 1$ elements of $A$, although they are not necessarily distinct.

cycle(环): A path that begins and ends at the same vertex is called a cycle(环).
It is clear that the paths of length $1$ can be identified with the ordered pairs $(x, y)$ that belong to $R$.
$R^n$: If $n$ is a fixed positive integer, we define a relation $R^n$ on $A$ as follows: $x \ R^n \ y$ means that there is a path of length $n$ from $x$ to $y$ in $R$. 即存在一条x -> y的长度为n的路径.
- $R^n(x)$ consists of all vertices that can be reached from $x$ by means of a path in $R$ of length $n$.
$R^∞$: The connectivity(连通性) relation $R^∞$ of a relation $R$ on a set $A$ mean that if by letting $x R^∞ y$, there is some path in $R$ from $x$ to $y$. $R^∞$ 也被称为connectivity(连通性). 即存在一条x -> y的长度未知的路径.
- The set $R^∞(x)$ consists of all vertices that can be reached from $x$ by some path in $R$.
$R^*$: The reachability(可达性) relation $R^*$ of a relation $R$ on a set $A$ that has $n$ elements is defined asfollows:

$x \ R^∗ \ y$ means that $x=y$ or $x \ R^∞ \ y$. The idea is that $y$ is reachable from $x$ if either $y$ is $x$ or there is some path from $x$ to $y$. y到x是可达的 = 要么y就是x, 要么存在一条x -> y的长度未知的路径.
- It is easily seen that $M_{R^∗} = M_{R^∞} ∨ I_n$, where $I_n$ is the $n × n$ identity matrix.
路径的组合:

Let $π_1: a,x_1,x_2,\cdots,x_{n−1},b$ be a path in a relation $R$ of length $n$ from $a$ to $b$, and let $π_2 : b,y_1,y_2,...,y_{m−1},c$ be a path in $R$ of length $m$ from $b$ to $c$.

Then the composition of $π_1$ and π2 $π_2$ the path $a,x_1,x_2,...,b,y_1,y_2,...,y_{m−1},c$ of length $n+m$, which is denoted by $π_2 ◦π_1$. This is a path from $a$ to $c$.

即: 如果有一条长度为m的路径$π_1$: a -> ... -> b, 长度为n的路径$π_2$: b -> ... -> c. 则存在从a到c的路径a -> ... -> b -> ... -> c, 它是$π_1$和$π_2$的组合, 长度为m+n.

Theorem:

If $R$ is a relation on $A=\{a_1,a_2,...,an\}$, then $M_{R^2} = M_R ⊙ M_R$

Proof:
Let $M_R = m_{ij}$ and $M_{R^2} = n_{ij}$ . By definition, the $i, j$th element of is $M_R ⊙ M_R$ equal to $1$ if and only if row $i$ of $M_R$ and column $j$ of $M_R$ have a $1$ in the same relative position, say position $k$. This means that $m_{ik} = 1$ and $m_{kj} = 1$ for some $k, 1 ≤ k ≤ n$.

By definition of the matrix $M_R$, the preceding conditions mean that $a_i \ R \ a_k$ and $a_k \ R \ a_j$. Thus $a_i \ R^2 \ a_j$, and so $n_{ij} = 1$. We have therefore shown that position $i, j$ of $M_R ⊙ M_R$ is equal to $1$ if and only if $n_{ij} = 1$. This means that $M_R ⊙ M_R = M_{R^2}$ .

翻译:

如果$M_R ⊙ M_R$ 的i,j元素为1, 当且仅当 $M_R$ 的第i行和$M_R$ 的第k列的对应位置(记为k)存在一个1, 即$m_{ik} = 1$ and $m_{kj} = 1$ for some $k, 1 ≤ k ≤ n$. 根据$M_R$ 的定义, 这意味着 $a_i \ R \ a_k$ and $a_k \ R \ a_j$, 因此存在长度为2的路径i->k->j, 因此有 $a_i \ R^2 \ a_j$, 所以有$n_{ij} = 1$.

这意味着: $M_R ⊙ M_R$ 的i,j元素为1 iff $n_{ij} = 1$. 也就是$M_R ⊙ M_R = M_{R^2}$ .

For brevity, we will usually denote $M_R ⊙ M_R$ . simply as $(M_R)^2_⊙$ (the symbol $⊙$ reminds us that this is not the usual matrix product).

Theorem:

之前的结论可以推导到n>=2:

For $n≥2$ and $R$ a relation on a finite set $A$, we have \[ M_{R^n} =M_R ⊙ M_R ⊙ \cdots ⊙ M_R \ (n \ \text{factors}). \] 证明略.

联系之前$R^*$的定义, 可得: \[ M_{R^*} =I_n \vee M_R \vee (M_R)_⊙^2 \vee (M_R)_⊙^3 \vee \cdots. \]

Equivalence Relations

equivalence relation(等价关系): A relation R on a set A is called an equivalence relation if it is reflexive, symmetric, and transitive. 即同时满足自反性, 对称性和传递性.

Example:

Let $A$ be the set of all triangles in the plane and let $R$ be the relation on $A$ defined as follows: \[ R=\{(a, b) \in A \times A \mid a \text { is congruent to } b\} . \] It is easy to see that $R$ is an equivalence relation.

Example:

Let $A=\{1,2,3,4\}$ and let \[ R=\{(1,1),(1,2),(2,1),(2,2),(3,4),(4,3),(3,3),(4,4)\} \] It is easy to verify that $R$ is an equivalence relation.

Equivalence Relations and Partitions

THEOREM 1: Equivalence Relation -> Partition

如果 $\mathcal{P}$ 是集合 $A$ 上的一个划分(partition), 那么可以用$\mathcal{P}$来构建一个等价关系.

Let $\mathcal{P}$ be a partition of a set $A$. Recall that the sets in $\mathcal{P}$ are called the blocks of $\mathcal{P}$. Define the relation $R$ on $A$ as follows: \[ a \ R \ b \quad \text{if and only if} \quad a \ \text{and} \ b \ \text{are members of the same block}. \]

Then $R$ is an equivalence relation on $A$.

Proof:

If $a \in A$, then clearly $a$ is in the same block as itself; so $a R a$. 自反性.
If $a R b$, then $a$ and $b$ are in the same block; so $b R a$. 如果$a R b$, 则a, b在同一个block内, 因此必定有$b R a$, 证明了对称性.
If $a R b$ and $b R c$, then $a, b$, and $c$ must all lie in the same block of $\mathcal{P}$. Thus $a R c$. 如果$a R b$, 则a, b在同一个block内, 同理b, c也在同一个block内, 因此a, b, c都在同一个block内, 因此有$a R c$. 证明了传递性.

因此 $R$ 是自反, 对称且传递的.

$R$ will be called the equivalence relation determined by $\mathcal{P}$.

Since $R$ is reflexive, symmetric, and transitive, $R$ is an equivalence relation.

THEOREM 2: Partition -> Equivalence Relation

反过来, 也可以用等价关系$R$ 来构建划分$\mathcal{P}$.

Let $R$ be an equivalence relation on $A$, and let $\mathcal{P}$ be the collection of all distinct relative sets $R(a)$ for $a$ in $A$.

Then $\mathcal{P}$ is a partition of $A$, and $R$ is the equivalence relation determined by $\mathcal{P}$.

Proof: According to the definition of a partition, we must show the following two properties:

Every element of $A$ belongs to some relative set(some $R(a)$).
If $R(a)$ and $R(b)$ are not identical, then $R(a) \cap R(b)=\varnothing$.

由于 $R$ 具有自反性, 我们有$a \in R(a)$ , 因此证明了性质1.

接着证明性质2的逆否命题: \[ \text{If} \quad R(a) \cap R(b) \neq \varnothing, \ \text{then} \ R(a)=R(b). \]

To prove this, we assume that $c \in R(a) \cap R(b)$. Then $a R c$ and $b R c$.

Since $R$ is symmetric, we have $c R b$.

Then $a R c$ and $c R b$, so, by transitivity of $R$, $a R b$.

Lemma1已经证明了$a \ R \ b \iff R(a)=R(b)$. 证明结束.

We have now proved that $\mathcal{P}$ is a partition. By Lemma 1 we see that $a R b$ if and only if $a$ and $b$ belong to the same block of $\mathcal{P}$. Thus $\mathcal{P}$ determines $R$, and the theorem is proved. Note the use of the contrapositive in this proof. If $R$ is an equivalence relation on $A$, then the sets $R(a)$ are traditionally called equivalence classes of $R$. Some authors denote the class $R(a)$ by $[a]$. The partition $\mathcal{P}$ constructed in Theorem 2 therefore consists of all equivalence classes of $R$, and this partition will be denoted by $A / R$. Recall that partitions of $A$ are also called quotient sets of $A$, and the notation $A / R$ reminds us that $\mathcal{P}$ is the quotient set of $A$ that is constructed from and determines $R$.

Lemma1

Let $R$ be an equivalence relation on a set $A$, and let $a \in A$ and $b \in A$. Then \[ a \ R \ b \quad \iff \quad R(a)=R(b) \]

Proof

充分性: 假设$R(a)=R(b)$, 由于$R$是自反的, 因此有 $b \in R(b)$, 因此有$b \in$ $R(a)$, 因此有$a R b$.

必要性:

假设 $a \ R \ b$. Then note that

由于 $R$ 是对称的, 所以有$b \ R \ a$.
$\forall x \in R(b)$, 有$ b R x$. 由于 $R$ 是传递的, 并且已经有$a \ R \ b$, 所以有$a \ R \ c$, 也就是说: $\forall x \in R(b), \ x \in R(a)$. 证明了 $R(b) \subseteq R(a)$.
反过来, $\forall y \in R(a)$, 有$ a R y$. 由于 $R$ 是传递的, 并且已经有$b \ R \ a$, 所以有$b \ R \ y$, 也就是说: $\forall y \in R(a), \ x \in R(a)$. 证明了 $R(a) \subseteq R(b)$.
综上所述, $R(a)=R(b)$.

Equivalence Class

equivalence class(等价类): If $R$ is an equivalence relation on $A$, then the sets $R(a)$ are traditionally called equivalence classes of $R$.

这里的$R(a)$指的是THEOREM2中的distinct relative set $R(a)$ for $a$ in $A$. 每个不同(distinct)的$R(a)$就是一个等价类.
划分 $\mathcal{P}$ 就是$R$的等价类构成的集合. $\mathcal{P}$ 被表示为$ A / R$.
由于$\mathcal{P}$也被称为A的商集(quotient set), the notation $A/R$ reminds us that $\mathcal{P}$ is the quotient set of $A$ that is constructed from and determines $R$.
Some authors denote the equivalence class $R(a)$ by $[a]$.

Transitive Closure and Warshall's Algorithm

Transitive Closure

In this section we consider a construction that has several interpretations and many important applications. Suppose that R is a relation on a set A and that R is not transitive. We will show that the transitive closure of R (see Section 7) is just the connectivity relation $R^{\infty}$, defined in Section 3.