Linked List Algorithms
Common Linked List Algorithms on Leetcode.
Reverse the Linkedlist
206. Reverse Linked List
92. Reverse Linked List II
Problem: 输入一个单链表头结点, 将该链表反转, 返回新的头结点.
Solution: 使用递归的方法, 先反转以head.next为head的子链表, 然后将原来的head拼接到子链表的末尾.
1 | /** |
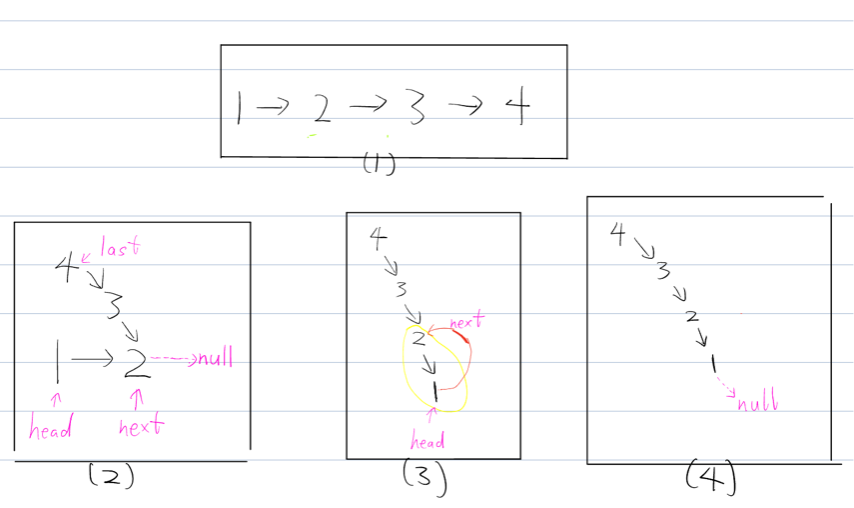
以上图为例:
如图(1), head为
1, 链表为1->2->3->4.如图(2), 递归思考, 将以
2为head的子链表2->3->4进行反转. 根据函数定义, 我们会得到反转后子链表4->3->2的头节点4, 记为last. 此时head.next依然为2, 即1->2.1
ListNode last = reverse_linked_list(head.next);
而由于
2已经是翻转后子链表的最后一个节点, 因此2->null.1
24(last)->3->2->null
1(head)-2->null接着把(1)变成最后一个节点, 即
4->3->2->1.1
head.next.next = head;
虽然
2的next变为1, 但1的next依然为2, 造成死循环:1
4(last)->3->2->1(->2->1->2->1->2->1....无限循环)
由于
1是翻转后链表的最后一个节点, 所以令1的next为null, 即4(last)->3->2->1(head)->null如图(4).1
head.next = null;
返回翻转后的整个链表的头节点, 它就是翻转后的子链表的头节点
last.1
return last;
Determine If Has A Cycle
141. Linked List Cycle
Given head, the head of a linked list, determine if the linked list has a cycle in it.
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail's next pointer is connected to. Note that pos is not passed as a parameter.
Return true if there is a cycle in the linked list. Otherwise, return false.
判断链表有无环的思路是快慢指针: 每当慢指针 slow 前进一步, 快指针 fast 就前进两步. 如果 fast 最终遇到空指针, 说明链表中没有环; 如果 fast 最终和 slow 相遇, 那肯定是 fast 超过了 slow 一圈, 说明链表中含有环.
1 | public boolean hasCycle(ListNode head) { |
Proof
下面证明快慢指针方法的正确性:
首先证明: 两指针相遇 => 链表存在环.
设两指针相遇的时间为t, t > 0. 则在t时刻, 慢指针slow的路程为t, 快指针fast的路程为2t.
使用反证法(证明逆否命题: 链表不存在环 => 两指针不能相遇), 如果链表不存在环, 则快慢指针的路径都是条直线. 两指针相遇 <=> 2t = t, 也就是 t = 0, 与前提t>0矛盾.
接下来证明: 链表存在环 => 两指针相遇.
假设链表list总长度为M, list[Q]为环的入口, 则环之前的长度为Q, 环的长度为M-Q. 由于链表存在环, 所以M-Q>0, 因此M > Q >= 0.
1 | {0 - > 1 - > 2 -> 3 -> ... -> Q-1} -> (Q -> ... -> M-1) |
设两指针相遇的时间为t, t > 0. 则在t时刻, 慢指针slow的路程为t, 快指针fast的路程为2t.
我们有如下断言:
- 如果两指针要相遇, 那么快指针必定在环内, 即有: 2t >= Q.
- 如果两指针要相遇, 那么快指针必定在环内至少循环了一次, 即存在k>=1使得: 2t - Q >= (M-Q)k.
(1), (2)的证明很简单, 如果快指针不在环内, 或者快指针在环内没有循环, 这种情况相当于链表不存在环, 而之前已经证明了链表不存在环 => 两指针不能相遇.
因此我们有如下约束:
t >= 1/2 Q
t >= 1/2 (M - Q)k + 1/2 Q
由于M>Q, 所以条件化简为: t >= 1/2 (M - Q)k + 1/2 Q
在这个条件下, 下面的式子代表两指针相遇:
(Note: 慢指针也在环中循环的情况也被包括在内, 因为k是任意取的>1的整数.)
t - Q = 2t - Q - (M-Q)k
t = (M-Q)k.
此时还需要满足 t >= 1/2 (M - Q)k + 1/2 Q, 需要:
(M-Q)k >= 1/2 (M - Q)k + 1/2 Q
即 k/2 (M-Q) >= 1/2 Q
M >= (k+1)/k Q
k >= 1/(M/Q - 1)
由于M > Q (意味着 M/Q > 1), 则对于任意的M,Q, 总存在k>=1使得k >= 1/(M/Q - 1), 此时的t = (M-Q)k满足:
t - Q = 2t - Q - (M-Q)k
使得双指针相遇.
即总存在t使得双指针相遇.
Get the Node where the Cycle Begins
142. Linked List Cycle II
Given the head of a linked list, return the node where the cycle begins. If there is no cycle, return null.
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail's next pointer is connected to (0-indexed). It is -1 if there is no cycle. Note that pos is not passed as a parameter.
Do not modify the linked list.
解法很简单, 使用单个指针遍历链表, 使用一个数据结构存储每个节点是否被访问过, 如果访问到了已经被访问过的节点, 则该节点就是环的起始点. 而如果指针指向到null, 说明该链表不存在环.
1 | public ListNode detectCycle(ListNode head) { |
Intersection of Two Linked Lists
160. Intersection of Two Linked Lists
Given the heads of two singly linked-lists headA and headB, return the node at which the two lists intersect. If the two linked lists have no intersection at all, return null.
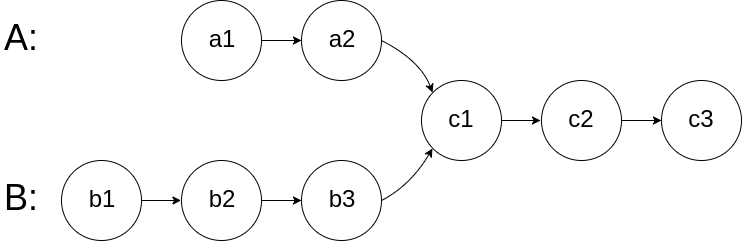
For example, the following two linked lists begin to intersect at node c1:
The test cases are generated such that there are no cycles anywhere in the entire linked structure.
Note that the linked lists must retain their original structure after the function returns.
和判断链表是否有环一样, 我们用两个指针p1, p2分别遍历链表A, B.
记链表A, B在公共节点前的长度为x, y, 公共节点的长度为z. 则A的长度为x+z, B的长度为y+z.
注意到: (x+z)+y = (y+z)+x
因此, 我们让p1在遍历完链表A(x+z)后再遍历链表B, p2在遍历完链表B(y+z)后再遍历链表A, 当p1, p2分别在B, A上走y, x步时, 两节点就会相遇, 该相遇的节点就是相交节点, 见下图:
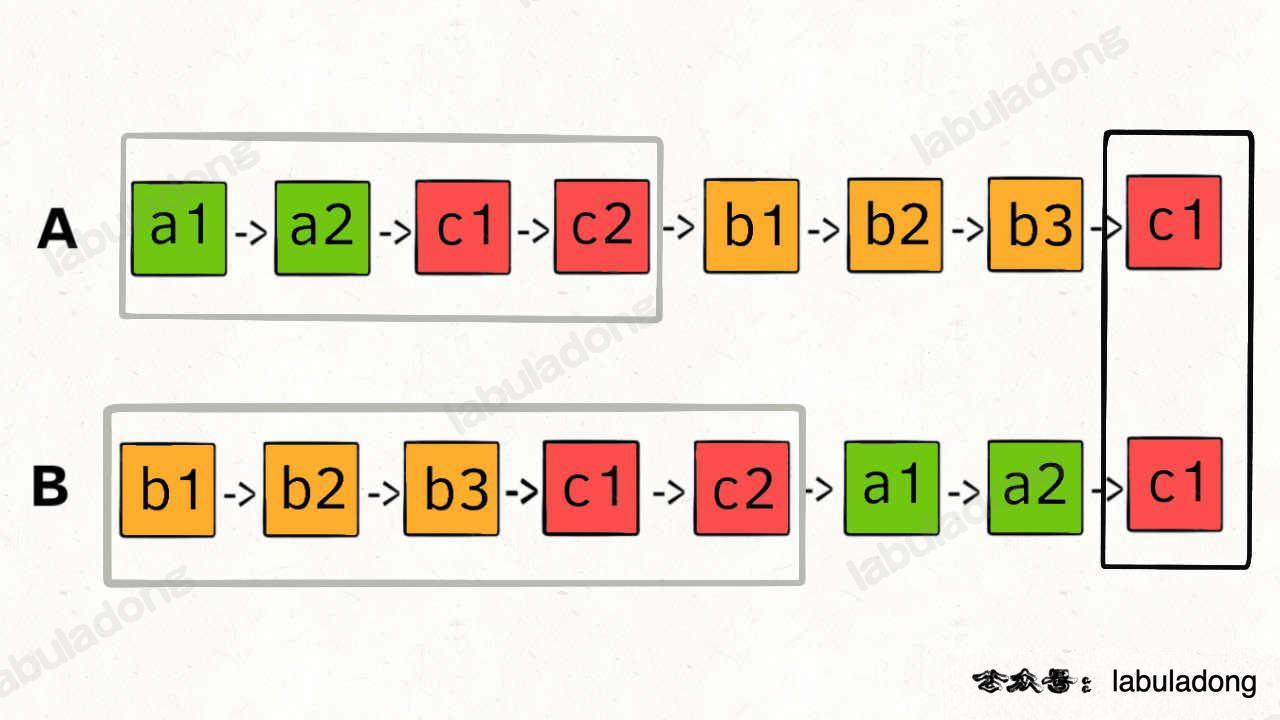
如果两条链表不相交, 此时z=0, 而p1, p2会在null处相遇, 返回null.
1 | public ListNode getIntersectionNode(ListNode headA, ListNode headB) { |