How Digital Cameras Work

Posted on Edited on In Views:

Outline:

  • Pixel's Color
  • Bayer Array
  • Interpolation/Approximation
  • Other applications of interpolation

Pixel's Color

在Resolution on Screen中, 我介绍了Pixel的概念. 我们也知道颜色是由红, 绿, 蓝 三原色组成的:

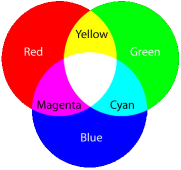
read, green, blue

每个像素都有颜色和亮度. 但是感光元件只能衡量亮度, 无法衡量光的波长(颜色), 要想感知色彩，需要在每个感光元件前加滤色片( filter ), 滤色片是单色的.

感光元件的材料有CCD (charge coupled device), and CMOS (complementary metal oxide semiconductor ). 对应人眼球的中央凹(当然中央凹不仅可以感知光的强度, 还能感知色彩)

  • 对于显示屏来说, 每个像素(感光元件)都是由三个红, 绿, 蓝的单色子像素(子感光元件)组成的.

  • 数码图像和显示器一样, 每个像素也由三个单色的子像素构成

  • 对于相机来说, 每个像素只是单色的, 缺失的另两种颜色从邻居“借来”

    • 照理来说可以像显示器一样, 将三个不同颜色的像素作为子像素合并为一个像素. 但是这样做效率很低, 对于相机而言不可接受.
    • 上面说法有个前提, 那就是感光元件使用Bayer Array.

Bayer Array

Uneven Distribution of Filters

相机的每个像素都有一个单色对Filter. 令人惊讶的是, Filter的数量是不均匀的.

其实, 人眼对于色彩的感知是不均匀的. 人眼的锥体( 大概6 million )有50%对绿色敏感, 25%对蓝色和红色敏感:

human eyes' color sensor distribution

Bryce Bayer根据这点发明了Bayer Array. 其中绿色Filter占50%, 红色和蓝色Filter各占25%:

Bayer Array 1
Bayer Array 2

由于简单好用, Bayer Array被绝大多数相机镜头采纳

Mind the Gap

下面介绍一下Bayer Array的成像步骤:

这是一张花的图片:

flower

框起来的区域:

flower area

我们要对框起来的区域使用bayer filter, 也就是单色的filter:

flower filter

这是输出的红色像素:

flower filter red

可以看到, 拥有红色Filter的像素大概占50%

这是绿色像素:

flower filter green

大概25%.

这是蓝色像素:

flower filter blue

大概25%.

将这三张像素图拼起来, 再结合它们对应的颜色:

就得到了:

flower output

可以看到, 结果图片还是很模糊的, 这是因为Bayer Array的像素都是单色的, 还缺失另外两原色. 对此, 我们需要采用数学手段, “猜出” 另外两原色.

Interpolation/Approximation

猜色问题可以抽象为: 已知两个点, 如何“猜出”它们的中间点. 这就是一个近似/插入问题.

对此, 我们有很多方法.

Nearest-neighbor

最简单的方法就是向邻居“借”颜色. 也就是中间点的取值 == 离中间点最近的点的取值.

在1维图像上, 就是这样:

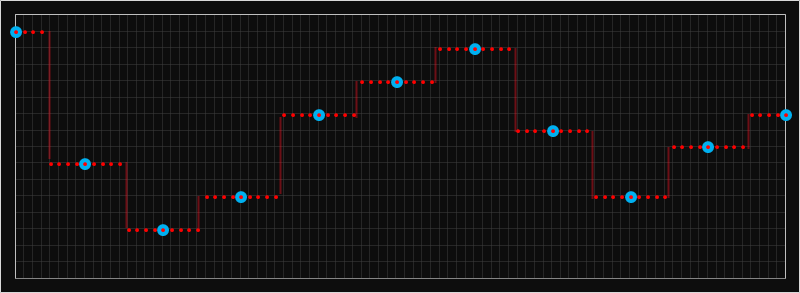
Nearest-neighbor 1D

二维图像是这样:

Nearest-neighbor 2D

对于相机的场景, 假设左图为原图, 右图采用了最近邻:

最近邻的优点是没有引入任何的虚拟值. 缺点是形成的图像成块状, 不够连续.

Linear

线性建模就是把已知点用直线连起来.

1维:

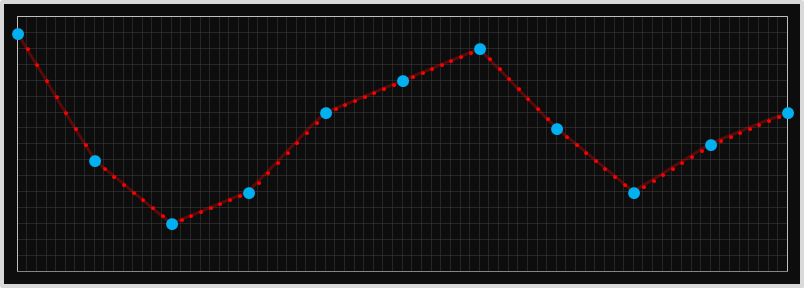
Linear 1D

2维:

Linear 2D

对于之前的相机的例子:

线性近似相比最近邻, 没有那么“blocky”. 但是如果图像有sharp edge, 用线性近似会把边界模糊掉

Quadratic

既然一阶的线性多项式效果不好, 不妨试试二阶. 二阶多项式需要三个点:

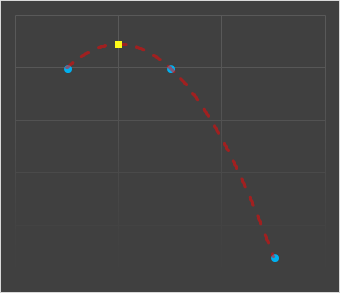
Quadratic

图中的黄色点就是二阶近似生成的

很可惜, 二阶近似没法使用, 因为:

  1. 图中可以看到, 二阶近似产生的中间值很可能过高或过低.
  2. 二阶方程没有拐点, 曲线不够平滑

Cubic

再试试四阶近似, 这需要四个点:

Cubic

1维:

Cubic 1D

3阶近似的效果不错. 但由于每次只考虑4个点, 前四个点的3阶方程曲线, 和后四个点的曲线, 可能会有比较大的差异. 所以在某些情况下, 3阶近似效果一般.

Catmull-Rom Splines

这是对3阶近似的一个改进. 依然需要4个点, 设为\(x_{-1},x_0, x_1, x_2\), 假设要求\(x_0, x_1\)的中间点, \(x_0, x_1\)中间曲线的三阶近似方程为: \[ \begin{align} f(x) = ax^3 + bx^2 + cx + d \nonumber \\ f'(x) = 3ax^2 + 2bx + c \nonumber \\ f'(x) = 3ax^2 + 2bx + c \nonumber \end{align} \] 我们已经知道了\(f(x_0), f(x_1)\), Catmull-Rom Splines要求设3阶方程在\(x_0, x_1\)处的斜率分别是直线\(x_{-1}x_1, x_0x_2\)的斜率. 也就是： \[ \begin{align} f'(x_0) = \frac {y_1 - y_{-1}}{2} \nonumber \newline f'(x_1) = \frac {y_2 - y_0}{2} \nonumber \end{align} \]

Catmull-Rom Splines

1维:

Catmull-Rom Splines 1D

2维:

img

相机:

img
camera pixels Catmull-Rom Splines

可以和普通的3阶近似做对比.

实践证明, Catmull-Rom Splines方法效果更好, 因此大部分相机都使用该算法.

General Case

对于像素填充问题, 我们只需要在两个点之间近似一个中间点就好了. 对于更一般的情况, 即在两个点之间近似一条曲线, 我们还有更多的方法.

Half-Cosine

取余弦函数曲线的一半, 它具有如下的“优秀”特性:

  1. 平滑
  2. 两端点处导数为0. 因此不会生成比已有值更高/低的近似值
Half-Cosine

1维:

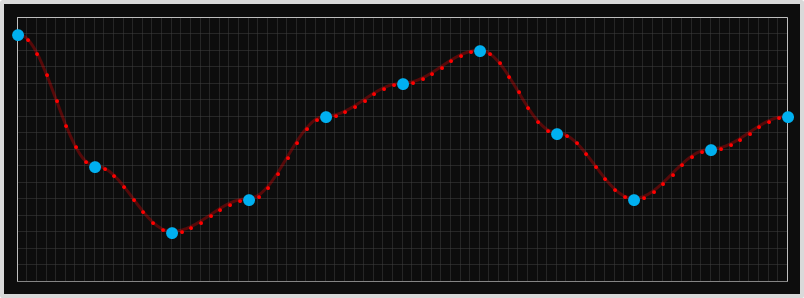
Half-Cosine 1D

不过, 由于\(\cos(\pi/4) = 1/2\), 对于求离散点的中点的情况, 其结果和线性近似一样. 所以对于相机像素的近似, 没必要用cos近似

Smoothstep

此外还可以将高阶多项式近似继续推广. Smoothstep只用于奇数阶多项式, 为了不产生过高/过低的估计值, 它假设段点处的高阶导数为0.

假设\(x \in [0,1], y \in [0,1]\), 已知\(f(0), f(1)\)

3阶Smoothstep就是3阶多项式, 并且其\(f'(0) = f'(1) = 1\)

5阶Smoothstep就是5阶多项式, 并且其\(f''(0) = f''(1) = f'(0) = f'(1) = 1\)

以此类推

Other applications of interpolation

Damping motion

前面介绍的近似方法可以应用在很多场景. 考虑一个点的直线运动的近似, 只有起点和终点两个已知点. 我们可以用:

  1. 最近邻
  2. 如果信息足够多的话, 已知点足够多, 比如有7个, 最近邻可以“好看”一点
  3. Half Cosine
  4. 3阶Smoothstep
  5. 5阶Smoothstep
  6. 7阶Smoothstep
velocity exp

可以看出不同的近似方法的差别

Ref

https://datagenetics.com/blog/may12018/index.html