L12 DAG

Posted on 2021-08-03 Edited on 2025-05-08 In Computer Science Views: 36

DAG(Directed Acyclic Graph), DAG's topological ordering and SCC(Strongly Connected Component).

Ref: 算法设计与分析(Algorithm design and analysis) by 黄宇.

Directed Acyclic Graph

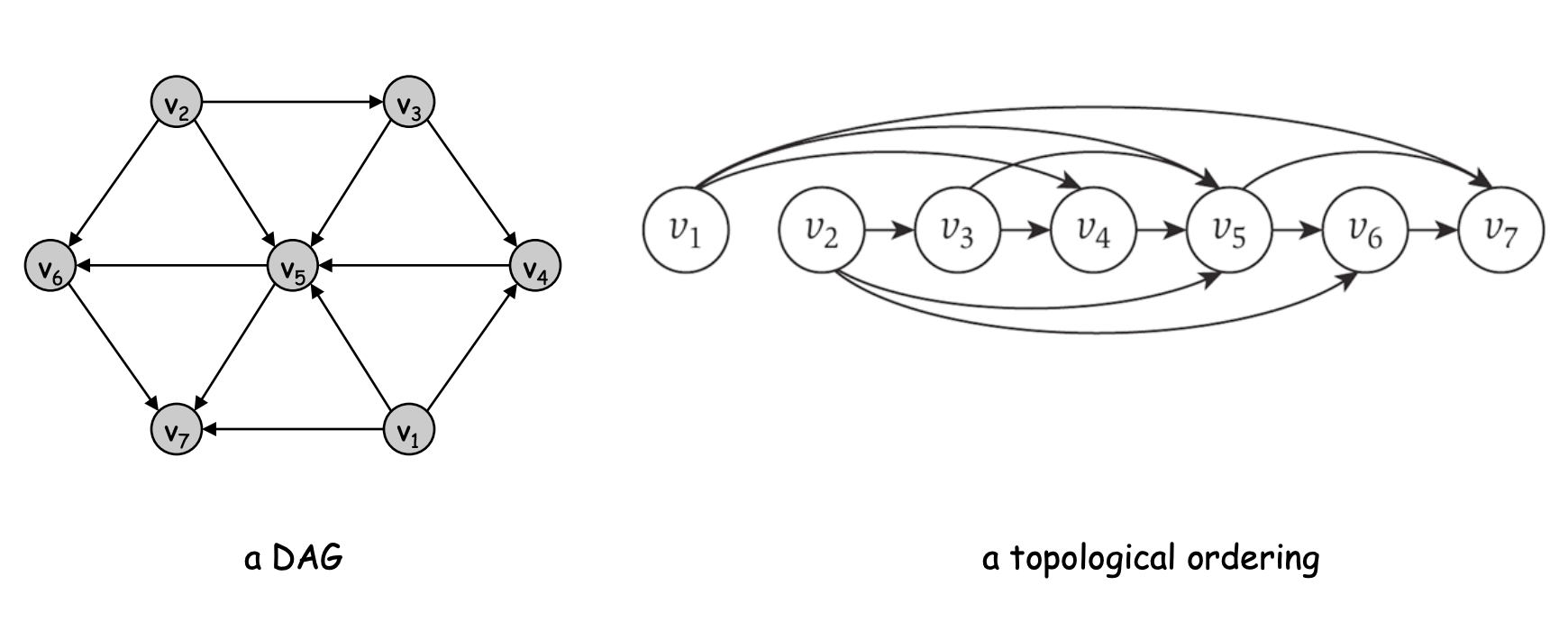
An DAG is a directed graph that contains no directed cycles.

Topological Ordering for G=(V,E)

A topological order of a directed graph $G = (V, E)$ is an assignment of distinct integer $1, 2, \dots, n$ of its nodes as $v_{1}, v_{2}, \dots, v_{n}$ so that for every edge $(v_{i}, v_{j}) \in E$ we have $i < j$ .

Lemma1

Lemma1: $G = (V, E)$ is a DAG <==> G has a topological order

Proof:

==> : (by induction on n)

Base case: true if n = 1.
Given DAG on n > 1 nodes, find a node v with no incoming edges.
G - { v } is a DAG, since deleting v cannot create cycles.
By inductive hypothesis, G - { v } has a topological ordering.
Place v first in topological ordering; then append nodes of G - { v } in topological order. This is valid since v has no incoming edges.

<== : (by contradiction)

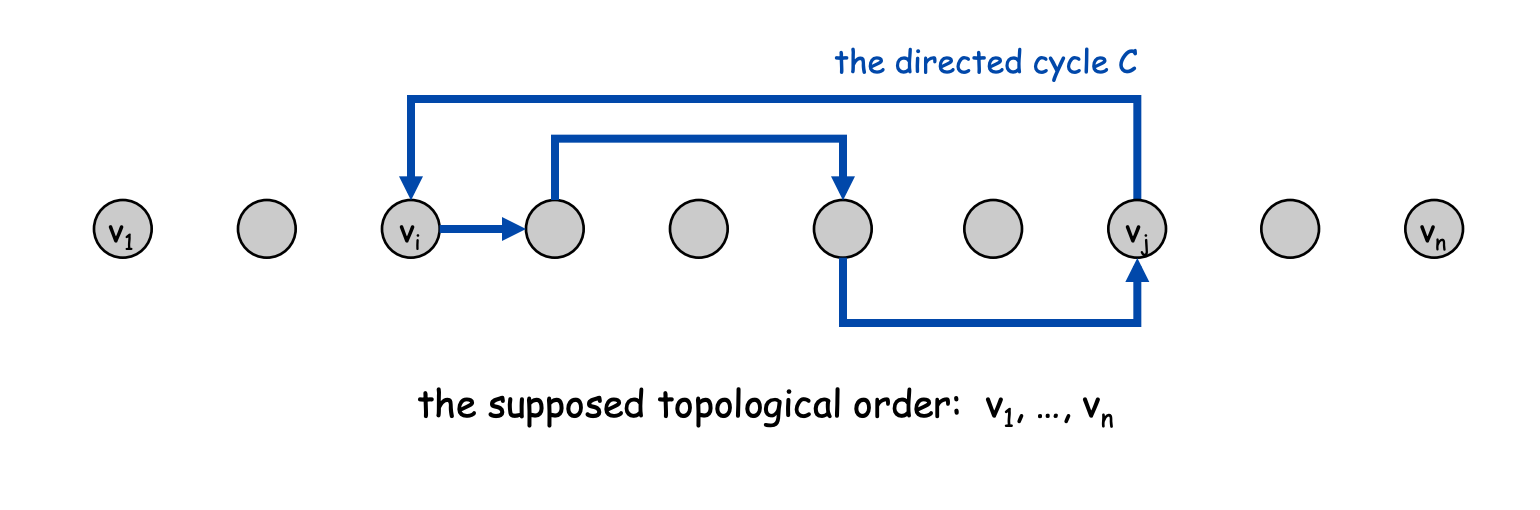
Suppose that G has a topological order v1, …, vn and that G also has a directed cycle C. Let's see what happens.
Let vi be the lowest-indexed node in C, and let vj be the node just before vi ; thus (vj, vi ) is an edge.
By our choice of i, we have i < j.
On the other hand, since (vj, vi ) is an edge and v1, …, vn is a topological order, we must have j < i, a contradiction.

Lemma2

Lemma2: If G is a DAG, then G has a node with no incoming edges.

Proof: (by contradiction)

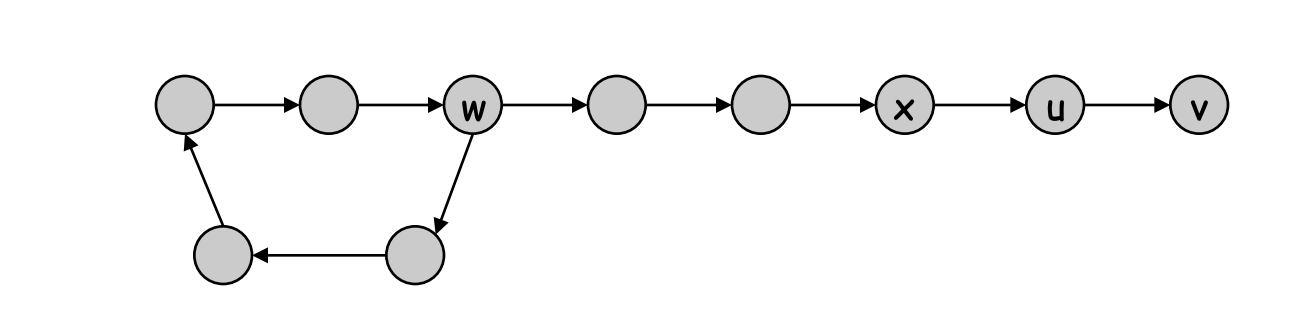
Suppose that G is a DAG and every node has at least one incoming edge. Let's see what happens.
Pick any node v, and begin following edges backward from v. Since v has at least one incoming edge (u, v) we can walk backward to u.
Then, since u has at least one incoming edge (x, u), we can walk backward to x.
Repeat until we visit a node, say w, twice.
Let C denote the sequence of nodes encountered between successive visits to w. C is a cycle.

Compute Topologic Ordering

在某个集合 $A$ 上的关系 $R$ 如果是自反的、反对称的和传递的，那么 $R$ 是一个偏序
偏序集的有向图中没有长度大于一的环
拓扑序要求全序且无环.
- 如果有向图 $G = (V, E)$ 有环, 则 $G$ 不存在拓扑排序.
- 成环等价于遍历过程中遇到了灰色节点.
"尽头"与DFS
- DFS就是沿某条路径一直往下走，直到某个“尽头”节点。
- 假设 $i \rarr j$ 表示任务 $i$ 的执行依赖任务 $j$ 的完成，则尽头节点不依赖其他任何节点，因而对它的拓扑序号的分配从依赖关系的角度看是自由的。该分配方式不会影响其他节点的执行. 比如，对于逆拓扑序而言，只要分配当前尚未分配的最小序号。
逻辑尽头
- 当一个节点的所有后续节点均已处理完毕时, 该节点就成为逻辑上的尽头节点。
  - 逆拓扑排序时, 逻辑尽头节点的逆拓扑序号只需要分配当前未分配序号中最小的
- 分配拓扑序号的过程就成为不断找到逻辑结点的过程,这与DFS适合
  - 在DFS-WRAPPER中,开始遍历之前定义一个全局变量globalNum, 并初始化为 n+1.
  - 在DFS框架的"遍历后处理"处,嵌入对拓扑排序的处理:
    - globalNum := globalNum -1.
    - v.topoNum := globalNum.
1
2
3
4
5
6
7
TOPO-WRAPPER(G)

globalNum = n+1;
Color all nodes WHITE;
foreach node v in G do
if v.color = WHITE then
TOPO-ORDER(v);
1
2
3
4
5
6
7
8
9
10
11
TOPO-ORDER(v)

v.color = GRAY;
foreach neighbour w of v do
if w.color = WHITE then
TOPO-ORDER(w);

globalNUM := globalNum - 1;
v.topoNum := globalNum;
v.color = BLACK;
Complexity: O(m+n). m = number of edges, n = number of vertices.

Critical path analysis

Critical path in a Task Graph

Earliest start time( est ) for a task v
- If v has no dependencies, the est is 0
- If v has dependencies, the est is the maximum of the earliest finish time of its dependencies.
Earliest finish time( left ) for a task v
- For any task: eft = est + duration
Critical path in a project is a sequence of tasks: $v_{0}, v_{1}, \dots, v_{k}$ , satisfying:
- $v_{0}$ has no dependencies;
- For any $v_{i}$ ( i = 1,2,...,k), $v_{i - 1}$ is a dependency of $v_{i}$ , such that est of $v_{i}$ equals eft of $v_{i - 1}$ ;
- eft of $v_{k}$ is maximum for all tasks in the project.
在DFS框架中嵌入相应处理
- 在"遍历前处理"处, 初始化该节点的最早开始时间, 并初始化关键路径相关信息
- 在结束邻接节点的处理返回的时候,检查是否要更新当前节点目前已知的最早开始时间.以及是否需要更新关键路径的相关信息
- 在"遍历后处理"处, 当前节点的est已确定, 则可以计算出当前节点的eft

CRITICAL-PATH(v) //该算法同样需要WRAPPER来调度
				 //逻辑尽头的est和est在其逻辑的关键路径中最小

v.color := GRAY
c.est := 0; v.CritDep := -1;
foreach neighbour w of v do
	if w.color = WHITE then
		CRITICAL-PATH(w);
	if w.eft >= v.est then
			v.est = w.eft //求efs的最大值
			v.CritDep := w;
			
v.eft := v.est + v.l;
v.color := BLACK;

Analysis

Complexity
- $Θ (n + m)$

Connectivity of DAG

Strongly Connected

强连通(strongly connected)： A DAG is strongly connected if every pair of nodes is mutually connected(->"connectivity" relation in graph).
- TL;DR: x和y是连通的 == 存在一条x -> y的长度未知的路径. (但长度不能为0)
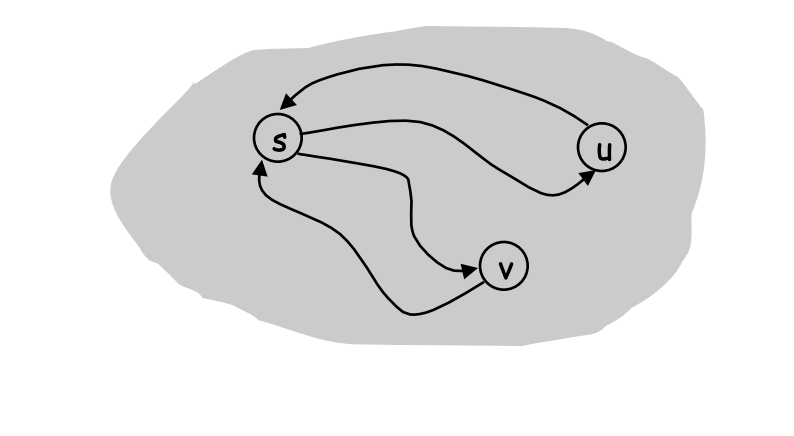
Lemma. Let s be any node. G is strongly connected iff every node is reachable from s, and s is reachable from every node.
Pf:

==> : Follows from definition.

<== :
1. Path from u to v: concatenate u-s path with s-v path.
2. Path from v to u: concatenate v-s path with s-u path.

Simply Connected

单连通(simply connected):A DAG is simply connected if 对图 G 中任意两个顶点 u 和 v, 存在从 u 到 v 的路径或从 v 到 u 的路径.

Weakly Connected

弱连通(weakly connected): A DAG is weakly connected if 忽略图 G 中每条有向边的方向, 得到的无向图（即有向图的基图）连通.

Detect Cycle in DAG

根据之前介绍的图的三种染色, 判断DAG是否有环就等价于判断在该图的遍历过程中是否遇到了灰色节点.

遇到灰色节点意味着在遍历该图时遇到了当前遍历树的祖先节点, 也就是成环.

public class Graph<T> {

    private List<Vertex<T>> vertices;

    public Graph() {
        this.vertices = new ArrayList<>();
    }

    //Some apis...
    
    public boolean hasCycle() {

        for(Vertex<T> vertex: vertices) vertex.setColor(Color.WHITE);//Every vertex hasn't been visited.

        for(Vertex<T> sourceVertex: vertices) {
            if(hasCycle(sourceVertex))
                return true;
        }
        return false;
    }

    private boolean hasCycle(Vertex<T> sourceVertex)
    {
        if(sourceVertex.getColor() == Color.GREY)//This vertex is being visited, we encounter a cycle!
            return true;
        if(sourceVertex.getColor() == Color.BLACK)//This vertex has been visited. So we don't need to traver it again.
            return false;

        sourceVertex.setColor(Color.GREY);//This vertex is being visited

        for (Vertex<T> neighbor : sourceVertex.getAdjacencyList()) {
            if( hasCycle(neighbor) )
                return true;
        }

        sourceVertex.setColor(Color.BLACK);//The visiting of this vertex is over. Color it black.
        return false;
    }
    

Strongly Connected Component（SCC）

Condensation Graph

Condensation Graph: 把G中的每个强连通片收缩成一个点, 强连通片之间的边收缩成一条有向边,则得到G的收缩图 $G ↓$
- 两个强连通片之间只能是单向可达(或者不可达).
- DAG的Condensation Graph还是DAG.

Traverse of SCC

SCC(G)

Initiate the empty stack nodeStack;

Perform DFS on G. In the postorder processing of each vertex v, insert the statement "nodeStack.push(v)"; //第一轮DFS,标记尽头,并通过栈完成排序

Compute the transpose grapg Gt of G;

Color all nodes WHITE;

while nodeStack != empty do
	v := nodeStack.pop();
	Conduct DFS from v on Gt;

Def:

For a DFS, the first vertex discovered in a strong component $S_{i}$ is called the leader of $S_{i}$ , 记为 $l_{i}$
推论：

The leader of $S_{i}$ is the last vertex to finish among all vertices of $S_{i}$ ( since all of them in the same DFS tree )( 即: 首节点的活动区间包含同一个强连通片中所有其他节点的活动区间 )
引理：
1. Each DFS tree of a digraph G contains only complete strong components of G, one or more.(即: 不可能一个强连通片中的节点一部分在某棵遍历树中,一部分不在)
2. $l_{i}$ 在第一轮遍历中被发现时(刚刚被处理,即将被染成灰色时), 不可能有路径通向某个灰色节点
  - Proof:
    
    反证法: 设 $S_{i}$ 的首节点 $l_{i}$ 刚被发现时, 有一条路径通向某个灰色节点x. 由于 $l_{i}$ 是首节点, 所以x必然处于图的另一个强连通片 $S_{j}$ 中(而不可能在 $S_{i}$ 中). 所以存在一条 $ S_i $到$ S_j $的路径 . 由于在$ l_i $刚被发现时, 节点 * x * 为灰色, 所以 * x * 为$ l_i $在 D F S T r e e 中的祖先节点 . 于是存在一条$ S_j $到$ S_i $的路径, 所以$ S_i $和$ S_j$是强连通的, 矛盾.
3. x(若有的话), 比 $l_{i}$ 先结束遍历, 即: x.finishTime < l.finishTime
  - x只能为白色或黑色
4. 在第二轮DFS中，当一个白色节点从栈中被POP出来时，它一定是其所在强连通片的首节点
  - Proof
    
    第二轮DFS时，一个出栈的节点 $l$ 为白色，则它必然是其所在强连通片 $S_{i}$ 的第一个出栈节点（否则就会在 $S_{i}$ 的其它先出栈的节点进行第二轮DFS时被染成灰色）。而在第一轮DFS时，最后一个入栈的节点就是最后结束的节点。而首节点 $l_{i}$ 的活动区间包含其他节点的活动区间，因而必然是最后结束的节点。所以 $l$ 必然是 $l_{i}$