L10 Union Find

Posted on Edited on In Views:

Union Find algorithm.

Ref:

  • 算法设计与分析(Algorithm design and analysis) by 黄宇
  • 并查集（Union-Find）算法 by labuladong

Problems about Union Find

Minimum Spanning Tree

  • Kruskal's algorithm, greedy strategy
    • Select one edge
      • With the minimum weight
      • Not in the tree
    • Evaluate this edge
      • This edge will NOT result in a cycle
  • Critical issue
    • How to know "NO CYCLE"?

Maze Generation

Black Pixels

Jigsaw Puzzle

Dynamic Equivalence Relation

  • Equivalence
    • 等价关系(自反, 对称, 传递)
    • 等价类们形成了一个划分(partition)
  • Dynamic equivalence relation
    • Changing in the process of computation
    • IS instruction: yes or no ( in the same equivalence class )
    • MAKE instruction: combining 2 equivalent classes by relating 2 unrelated elements, and influencing the results of subsequent IS instructions.
    • Starting as equality relation

Union-Find Based Algorithms

  • Maze Generation
    • Randomly delete a wall and union 2 cells
    • Loop until you find the inlet and outlet are in one equivalent class
  • The Kruskal's algorithm
    • Find whether u and v are in the same equivalent class
    • If not, add the edge and union the 2 nodes
  • Black Pixels
    • Find black pixel groups
    • How the union of black groups increases \(\alpha\)

Implementation: Choices

\(n\): 总元素个数，

\(m\): Find / Union 指令数

三种思路:

  • Matrix(relation matrix): Space in \(\Theta(n^2)\), and worst-case cost in \(O(mn)\)​ .
    • mainly for row copying for MAKE. m条指令，最坏情况下每条\(O(n)\)的代价.
  • Array( for equivalence class ID ): Space in \(\Theta(n)\)​, and worst-case cost in \(O(mn)\)​.
    • mainly for search and change for MAKE.
  • Forest of rooted trees:
    • A collection of disjoint sets, supporting Union and Find operations
    • Not necessary to traverse all the elements in one set

Union-Find

对于\(a\), \(b\), 定义等价关系\(R\)为: \[ a \ R \ b \quad \text{if and only if} \quad a \ \text{and} \ b \ \text{are members of the same block}. \] 使用的数据结构为Rooted Tree构成的森林, 每个Rooted Tree是划分的一个block(等价类), 使用树的根作为等价类的代表元来代表该等价类.

因此\(a\), \(b\) 位于同一个block就等价于\(a\), \(b\) 位于同一棵tree, 即\(a\), \(b\)的根相同:

\[ a \ R \ b \quad \text{if and only if} \quad a \ \text{and} \ b \ \text{have the same root}. \]

因此:

  • 对两个元素进行IS操作, 即判断它们是否属于同一个等价类 == 判断两个树的根是否相同. "两个树的根是否相同"是一个等价关系.
  • 对两个元素进行MAKE操作, 即将它们所属的等价类合并 == 将一个tree的根挂到另一个tree的根下面.
1
2
3
4
5
6
7
8
class UF {
    /* 将代表元 p 和 q 连接, 即MAKE操作 */
    public void union(int p, int q);
    /* 判断 p 和 q 是否connected, 即IS操作. connected关系是一个等价关系 */ 
    public boolean connected(int p, int q);
    /* 返回图中有多少个等价类 */
    public int count();
}

Implementation

Initiation

等价类的构建分两步:

  1. 初始化等价类.
  2. 之后对等价类的修改, 也就是MAKE操作.

在初始化部分, 每个节点都是单独的rooted tree. 由于等价关系具有自反性, 因此每个节点都有一条指向自己的长度为1的边, 即每个节点的parent都是自己:

img

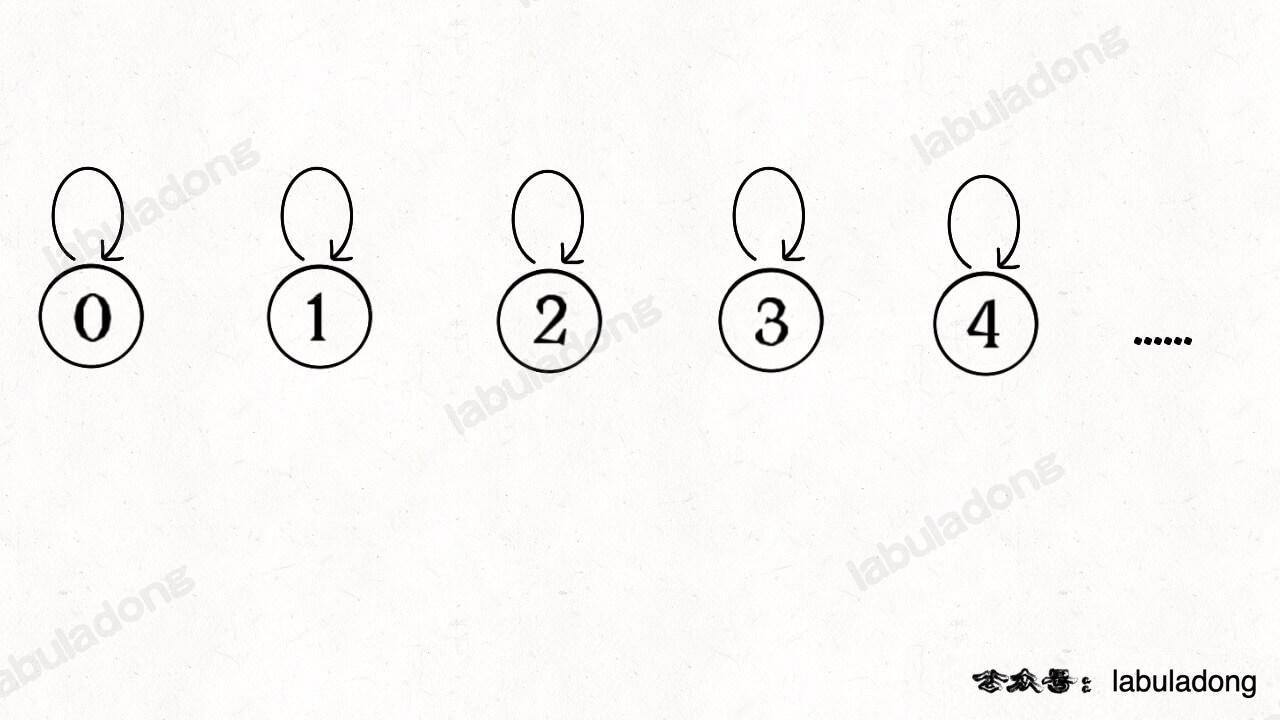
等价类的构建(初始化部分):

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class UF {
    // 记录连通分量
    private int count;
    // 节点 x 的父节点是 parent[x]
    private int[] parent;

    /* 构造函数，n 为图的节点总数 */
    public UF(int n) {
        // 一开始互不连通
        this.count = n;
        // 父节点指针初始指向自己
        parent = new int[n];
        for (int i = 0; i < n; i++)
            parent[i] = i;
    }

    /* 其他函数 */
}
  • 开销: 对\(n\)个节点都处理一遍, 开销为\(n\).

find()

查找元素所在等价类的代表元:

1
2
3
4
5
6
7
8
9
10
/* 返回某个节点 x 的根节点, 即x所在等价类的代表元 */
private int find(int x)
{
    // 根节点root具有的特性: parent[root] == root
    while(x != parent[x])
    {
        x = parent[x];
    }
    return x;
}

IS

IS操作即代码的boolean connected(int p, int q)函数, 对于两个元素, 分别找到其等价类的代表元, 也就是树的根, 然后判断两个根是否相同:

\(\mathrm{IS}( p, q )\):

  1. \(t = find(p)\)
  2. \(u = find(q)\)
  3. \((t == u)\)​ ?
1
2
3
4
5
6
7
/* 判断 p 和 q 是否connected, 即IS操作. connected关系是一个等价关系 */ 
public boolean connected(int p, int q){
	int rootP = find(p);
	int rootQ = find(q);

	return rootP==rootQ;
}
  • 开销: 两次find()

MAKE

MAKE操作即代码的boolean connected(int p, int q)函数, 对于两个元素, 分别找到其等价类的代表元, 也就是树的根, 然后将一个root挂到另一个root下面.

\(\mathrm{MAKE}( p, q )\):

  1. \(t = find(p)\)
  2. \(u = find(q)\)
  3. \(union(t,u)\)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
/**
* connect p and q. The new root will be p's root.
*/
public void union(int p, int q)
{
	int rootP = find(p);
	int rootQ = find(q);

	if( rootP == rootQ )
		return;
	else
	{
		// 将两棵树合并为一棵
		parent[rootQ] = rootP;
		count--;// 两个等价类合而为一
	}
}
  • 开销: 两次find().

Critical Operation

并查集(UF)的critical operation: 等价类(rooted tree)的构建(assignment)和查找(lookup). 称作 "link operation".

  • 构建: 指定某节点都父节点.

    1
    parent[x] = p;

  • 查找: 查询某节点的父节点.

    1
    p = parent[x];

我们假定每次link operation的复杂度为 \(O(1)\)

Worst-case Analysis

  • 最坏开销在在根树极度不均衡时出现, 此时根树变成一个链表.

    • 将每个元素都初始化为等价类, 开销为n.
    • 一共有n-1次MAKE. 每次MAKE都会调用常数次find(), 由于树的深度随着MAKE的次数增加, find()的开销也随之增加, 为1, 2, 3, ..., n-1.
    • 由于总共有m条指令, 因此IS次数就是(m-n+1). 每次IS都会调用常数次find(). 由于树已经被构建完毕, 考虑最坏情况, 即每次都查最深的那个, 则每次find()的复杂度都为n.

  • 最坏开销为 \[ n + O(n^2) + O((m-n+1)n) = \Theta(mn) \]

    和蛮力策略代价一样,这是因为并查操作都太简单了, 没有特殊约束.

  • 可以看到, 除了并查集的初始化(需要n的开销), 并查集的所有操作只有MAKE和IS, 其开销都等于两次find(), 因此优化并查集 == 优化find().

Optimization

Weight Union

平衡性优化.

img

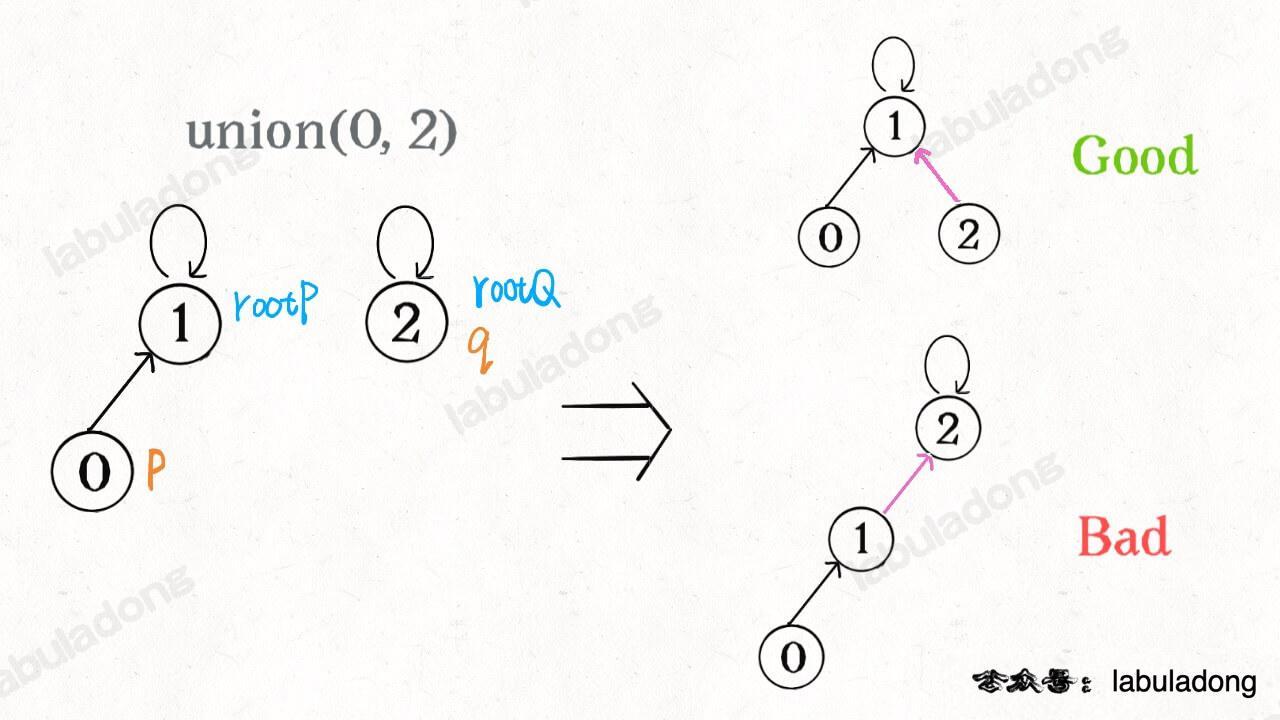
之前的MAKE操作简单地把 p 所在的树接到 q 所在的树的根节点下面, 这就可能出现「头重脚轻」的不平衡状况, 比如上面这种局面.

在这种情况下, 对构建后的rooted tree的每次find()的开销都是\(O(n)\).

解决办法: Weight union( wUnion )

  • always have the tree with fewer nodes as subtree. 把小一些的树接到大一些的树下面，这样就能避免头重脚轻，更平衡一些.

额外使用一个 size 数组，记录每棵树包含的节点数，我们不妨称为「重量」：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class UF {
    private int count;
    private int[] parent;
    // 新增一个数组记录树的“重量”
    private int[] size;

    public UF(int n) {
        this.count = n;
        parent = new int[n];
        // 最初每棵树只有一个节点
        // 重量应该初始化 1
        size = new int[n];
        for (int i = 0; i < n; i++) {
            parent[i] = i;
            size[i] = 1;
        }
    }
    /* 其他函数 */
}

比如说 size[3] = 5 表示，以节点 3 为根的那棵树，总共有 5 个节点。这样我们可以修改一下 union 方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class UF {
    // 为了节约篇幅，省略上文给出的代码部分...

    public void union(int p, int q) {
        int rootP = find(p);
        int rootQ = find(q);
        if (rootP == rootQ)
            return;
        
        // 小树接到大树下面，较平衡
        if (size[rootP] > size[rootQ]) {
            parent[rootQ] = rootP;
            size[rootP] += size[rootQ];
        } else {
            parent[rootP] = rootQ;
            size[rootQ] += size[rootP];
        }
        count--;
    }
}
  • 解决树的平衡性问题,为什么不用height, 而要用size?
    • 其实也有用height的优化Union方案,这里没教
    • 由于在用size的方案中, "size小而height大"这种反例不可能出现,所以size方案是可行的
  • 使用wUnion后, 树的深度保持在\(\log n\), 即find()复杂度为\(\log n\).

Worst case Analysis

  • 任意次wUnion后, \(n\)个节点的根树的高度上界是 \(\lfloor logn \rfloor\)​
  • 证明用归纳法
  • A Union-Find program of size m, on a set of n elements, performs \(\Theta(m + n\lfloor logn \rfloor)\)​​ link operations in the worst case if wUnion and straight find are used
  • Proof:
    • At most \(n-1\) wUnion can be done, building a tree with height at most \(\lfloor logn \rfloor\)
    • Then, each find costs at most \(\lfloor logn \rfloor + 1\)
    • Each wUnion costs in \(O(1)\), so, the upper bound on the cost of any combination of m wUnion/find operations is the cost of m find operations, that is \(m(\lfloor logn \rfloor + 1) \in O(n+ m\lfloor logn \rfloor)\)

Path Compression Find

路径压缩.

img

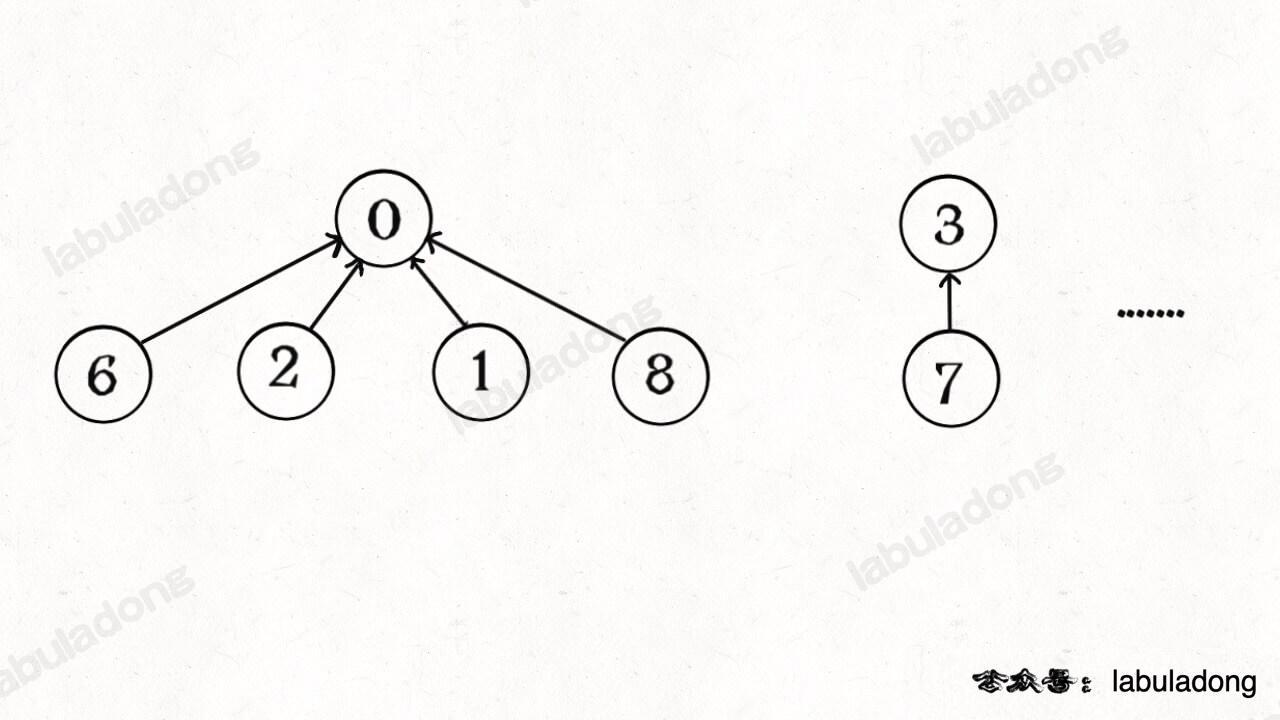
其实, 在并查集中, 我们不在乎树的结构, 只在乎根节点.

解决办法: Path Compression Find(cFind)

  • 将树的高度压缩到常数, 最好的自然是2.
  • 通过把高度压缩到2, 每个节点的父节点就是整棵树的根节点, find() 的复杂度就是\(O(1)\). 相应的, IS和MAKE复杂度都下降为 O(1).

新的find()方法用递归实现:

1
2
3
4
5
6
7
8
9
10
11
12
class UF {
    // 为了节约篇幅，省略上文给出的代码部分...
    
    // 第二种路径压缩的 find 方法
    public int find(int x) {
        if (parent[x] != x) {
            parent[x] = find(parent[x]);
        }
        return parent[x];
    }
}

  • 每当tree的结构发生变动, 则新的第一次find()会花费n的时间来进行路径压缩, 后续所有find()的开销都为1. 这样的开销比wUnion更低.
  • 注意: 由于cFind会将树的高度压缩为2, 因此实际上没有必要再用wUnion了.

Worst case Analysis

(以下分析是针对老师讲的cFind的, 和我上面写的版本不一样. 我的cFind是常数开销, 因此不需要和wUnion结合.)

  • 用平摊分析, cFind是昂贵操作(仅指第一次).
  • (使用wUnion和cFind)代价是\(O((n+m)log^*(n))\)​
    • \(log^*n\)的反函数是n个2叠罗汉,后者增长很快,因此前者增长很慢, 可以近似看作常数
      • Log-star grows extremely slowly \(\lim\limits _{n \rarr \infty} { \frac {log^* n} {log ^{(p)} n}}\), p is any nonnegative constant​​
  • 平摊分析的细节不讲了